题目内容
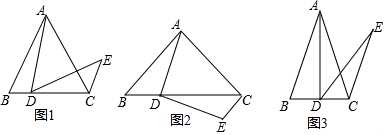
7.△ABC和△ADE中,AB=AC,DA=DE,∠BAC=∠ADE=α,点D在BC上,连接CE(1)如图1,若α=60°,则∠DCE=120°;
(2)如图2,若α=90°,求∠DCE的度数;
(3)如图3,若0°<α<60°,直接写出∠DCE的度数(用含α的式子表示)
分析 (1)如图1,根据已知条件得到△ABC与△ADE是等边三角形,根据等边三角形的性质得到∠BAC=∠DAE=60°,根据全等三角形的性质得到∠B=∠ACE=60°,于是得到结论;
(2)根据已知条件得到∠ACD=∠AED=45°,求得∠ECO=∠DAO=45°,推出点A,C,E,D四点共圆,根据圆内接四边形的性质得到∠ACE+∠ADE=180°,于是得到结论;
(3)连接AE,根据等腰三角形的性质得到∠ACD=∠AED=$\frac{1}{2}$(180°-α),又推出 点A,D,C,E四点共圆,根据圆周角定理得到∠ACE=∠ADE=α,于是得到结论.
解答 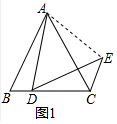 解:(1)如图1,∵AB=AC,DA=DE,∠BAC=∠ADE=60°,
解:(1)如图1,∵AB=AC,DA=DE,∠BAC=∠ADE=60°,
∴△ABC与△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAD=∠EAC,AE=AD,
在△ABD与△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△CAE,
∴∠B=∠ACE=60°,
∴∠DCE=∠ACB+∠ACE=120°,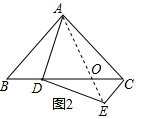
故答案为:120°;
(2)∵等腰△ABC和等腰△ADE中,AB=AC,AD=DE,∠BAC=∠ADE=90°,
∴∠ACD=∠AED=45°,
∴∠ECO=∠DAO=45°,
∴点A,C,E,D四点共圆,
∴∠ACE+∠ADE=180°,
∵∠ADE=90°,
∴∠ACE=90°,
∴∠DCE=45°,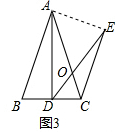
(3)连接AE,
∵AB=AC,AD=DE,∠BAC=∠ADE=α,
∴∠ACD=∠AED=$\frac{1}{2}$(180°-α),
∴点A,D,C,E四点共圆,
∴∠ACE=∠ADE=α,
∴∠DCE=∠ACD+∠ACE=$\frac{1}{2}$(180°-α)+α=90°+$\frac{1}{2}α$.
点评 本题主要考查了四点共圆,等腰三角形的性质,正确的作出辅助线是解题的关键.

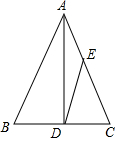 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
| A. | 80 | B. | 4 | C. | 16 | D. | 2 |
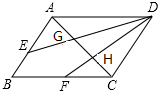 如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.
如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.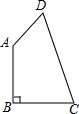 如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.
如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.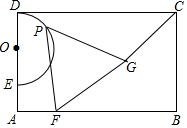 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.
如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.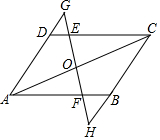 如图.在?ABCD中,点E、F分别在DC、AB上,DE=BF,直线EF分别与AD、CB的延长线相交于点G、H.求证:AC、GH互相平分.
如图.在?ABCD中,点E、F分别在DC、AB上,DE=BF,直线EF分别与AD、CB的延长线相交于点G、H.求证:AC、GH互相平分.