题目内容
12.把下列各数填在相应的大括号里.8,-|-2|,0,-1.04,-(-10),$\frac{22}{7}$,-$\frac{1}{3}$,+$\frac{3}{4}$.
正整数集合:{8,-(-10)…};
整数集合:{8,-|-2|,0,-(-10)…};
正分数集合:{$\frac{22}{7}$,+$\frac{3}{4}$…};
负分数集合:{-1.04,-$\frac{1}{3}$…}.
分析 按照有理数的分类填写:
有理数$\left\{\begin{array}{l}整数\left\{\begin{array}{l}正整数\\ 0\\ 负整数\end{array}\right.\\ 分数\left\{\begin{array}{l}正分数\\ 负分数\end{array}\right.\end{array}\right.$.
解答 解:正整数集合:{ 8,-(-10)};
整数集合:{ 8,-|-2|,0,-(-10)};
正分数集合:{ $\frac{22}{7}$,+$\frac{3}{4}$};
负分数集合:{-1.04,-$\frac{1}{3}$};
故答案为:8,-(-10);8,-|-2|,0,-(-10);$\frac{22}{7}$,+$\frac{3}{4}$;-1.04,-$\frac{1}{3}$.
点评 本题考查了有理数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.下列命题中,假命题的个数是( )
①垂直于半径的直线一定是这个圆的切线;
②圆有且只有一个外切三角形;
③三角形有且只有一个内切圆;
④三角形的内心到三角形的三个顶点的距离相等.
①垂直于半径的直线一定是这个圆的切线;
②圆有且只有一个外切三角形;
③三角形有且只有一个内切圆;
④三角形的内心到三角形的三个顶点的距离相等.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.现有A,B两枚均匀的小立方体骰子,每个面上分别标有数字1,2,3,4,5,6.如果由小李同学掷A骰子朝上面的数字x,小明同学掷B骰子朝上面的数字y来确定点P的坐标(x,y),那么他们各掷一次所确定的点P落在已知直线y=-x+8的概率是( )
| A. | $\frac{5}{36}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{36}$ | D. | $\frac{1}{9}$ |
4.下列说法正确的是( )
| A. | 有理数是指整数、分数、正数、负数和0 | |
| B. | 0是整数,但不是自然数 | |
| C. | 在有理数中,不是正数就是负数 | |
| D. | 一个有理数不是整数就是分数 |
2.一个数加上-1得-5,那么这个数为( )
| A. | 4 | B. | -4 | C. | -6 | D. | 65 |
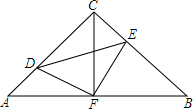 如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.
如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16. 如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.
如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.