题目内容
3. 如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,求证:AE2+BE2=2CE2.(多种方法解答)
如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,求证:AE2+BE2=2CE2.(多种方法解答)
分析 连结AD,由于△ABC和△DCE都是等腰直角三角形,那么∠B=∠BAC=45°,AC=BC,CE=CD,∠ACB=∠DCE=90°,结合等式性质易证∠1=∠2,那么利用SAS可证△ACD和△BCE,于是可得∠CAD=∠B=45°,易求∠EAD=90°,再利用勾股定理可得AE2+BE2=2CE2.
解答 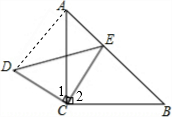 证明:连结AD,∵△ABC和△DCE都是等腰直角三角形,
证明:连结AD,∵△ABC和△DCE都是等腰直角三角形,
∴∠B=∠BAC=45°,AC=BC,CE=CD,∠ACB=∠DCE=90°,
∴∠ACB-∠ACE=∠DCE-∠ACE,
即∠1=∠2,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠1=∠2}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠B=45°,AD=BE,
∴∠EAD=∠DAC+∠CAB=45°+45°=90°,
∴AE2+BE2=AE2+AD2=DE2=2CE2.
点评 本题考查了全等三角形的判定和性质、等腰直角三角形的性质、勾股定理,解题的关键是证明△AC口≌△BCE.

练习册系列答案
相关题目
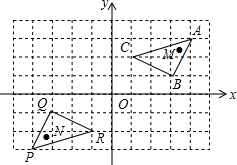 如图,△PQR是三角形ABC经过某种变换后得到的图形.
如图,△PQR是三角形ABC经过某种变换后得到的图形.