题目内容
如图，在△ABC中，AB=5，AC=13，BC边上的中线AD=6，求证：△ABD为直角三角形．考点：全等三角形的判定与性质,勾股定理的逆定理
专题：证明题
分析：延长AD到点E，使DE=AD=6，连接CE，可证明△ABD≌△CED，所以CE=AB，再利用勾股定理的逆定理证明△CDE是直角三角形即：△ABD为直角三角形．
解答：证明：延长AD到点E，使DE=AD=6，连接CE
，
∵AD是BC边上的中线，
∴BD=CD，
在△ABD和△CED中，
，
∴△ABD≌△CED（SAS），
∴CE=AB=5，∠BAD=∠E，
∵AE=2AD=12，CE=5，AC=13，
∴CE2+AE2=AC2，
∴∠E=90°，
∴∠BAD=90°，
即△ABD为直角三角形．
，∵AD是BC边上的中线，
∴BD=CD，
在△ABD和△CED中，
|
∴△ABD≌△CED（SAS），
∴CE=AB=5，∠BAD=∠E，
∵AE=2AD=12，CE=5，AC=13，
∴CE2+AE2=AC2，
∴∠E=90°，
∴∠BAD=90°，
即△ABD为直角三角形．
点评：本题考查了全等三角形的判定和性质、勾股定理的逆定理的运用，解题的关键是添加辅助线，构造全等三角形，题目的设计很新颖，是一道不错的中考题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
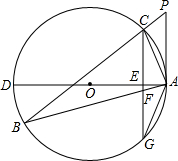如图，△ABC为⊙O的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD交AD于E，交AB于F，交⊙O于G．