题目内容
解方程:
+
=4.
| 3x |
| x2+1 |
| x2+1 |
| x |
考点:换元法解分式方程
专题:
分析:可根据方程特点设y=
,则原方程可化为y2-4y+3=0.解一元二次方程求y,再求x.
| x |
| x-1 |
解答:解:设y=
,
得:
+y=4,
y2-4y+3=0,
解得y1=1,y2=3.
当y1=1时,
=1,x2-x+1=0,此方程没有数解.
当y2=3时,
=3,x2-3x+1=0,解得x=
.
经检验x=
都是原方程的根,
所以原方程的根是x=
.
| x2+1 |
| x |
得:
| 3 |
| y |
y2-4y+3=0,
解得y1=1,y2=3.
当y1=1时,
| x2+1 |
| x |
当y2=3时,
| x2+1 |
| x |
3±
| ||
| 2 |
经检验x=
3±
| ||
| 2 |
所以原方程的根是x=
3±
| ||
| 2 |
点评:本题考查用换元法解分式方程的能力.用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
相关题目
在数4,-1,3,-6中,其中最小的是( )
| A、-6 | B、-4 | C、-1 | D、6 |
若直角三角形两直角边的边长分别是5和12,则斜边上的高为( )
| A、6 | ||
B、
| ||
C、
| ||
D、
|
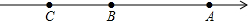 如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=
如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB= 如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
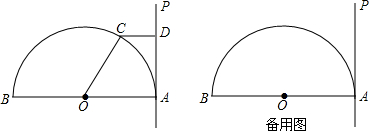
 如图,在⊙O中,点C是
如图,在⊙O中,点C是