题目内容
10．如果两个相似三角形面积的比为3：5，那么它们的相似比为$\frac{\sqrt{15}}{5}$．分析 根据相似三角形的面积的比等于相似比的平方得到它们的相似比=$\sqrt{\frac{3}{5}}$，然后化简即可．
解答 解：∵两个相似三角形面积的比为3：5，
∴它们的相似比=$\sqrt{\frac{3}{5}}$=$\frac{\sqrt{15}}{5}$．
故答案为$\frac{\sqrt{15}}{5}$．
点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比；相似三角形的面积的比等于相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
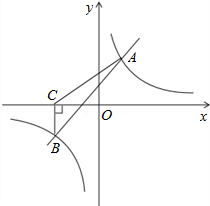如图，函数y=x+b与y=$\frac{k}{x}$相交于点A（2，n）和点B（3-2n，-2）．
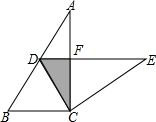如图，Rt△ABC中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转一定角度后得△EDC，点D在AB边上，斜边DE交AC于点F，则图中阴影部分面积为$\frac{\sqrt{3}}{2}$．
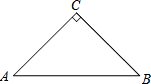如图，等腰Rt△ABC中，AC=BC，AB=2，将线段AB绕A点逆时针方向旋转，B点的对应点为D，若CD∥AB，则CD的长为$\sqrt{3}$+1或$\sqrt{3}$-1．
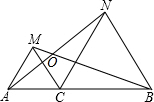如图，点C为线段AB上一点，△ACM，△CBN是等边三角形，求证：AN=BM．
如图所示，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，问：∠1和∠2相等吗？请说明理由．
2．点P与点Q（-3，2）关于原点对称，则点P的坐标是（ ）
| A． | （-3，2） | B． | （2，-3） | C． | （3，-2） | D． | （-2，3） |
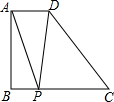如图，已知梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P为BC边上一个动点，连接PA、PD，则△PAD周长的最小值是2$\sqrt{17}$+2．
20．
如图，在?ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE的长为（ ）
如图，在?ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE的长为（ ）| A． | 2cm | B． | 3cm | C． | 6cm | D． | 8cm |