题目内容
18.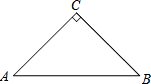 如图,等腰Rt△ABC中,AC=BC,AB=2,将线段AB绕A点逆时针方向旋转,B点的对应点为D,若CD∥AB,则CD的长为$\sqrt{3}$+1或$\sqrt{3}$-1.
如图,等腰Rt△ABC中,AC=BC,AB=2,将线段AB绕A点逆时针方向旋转,B点的对应点为D,若CD∥AB,则CD的长为$\sqrt{3}$+1或$\sqrt{3}$-1.
分析 作AD⊥CD,垂足为E,易求AE=1,根据旋转的性质知AD=AB=2,所以DE=$\sqrt{3}$,CE=1,当点D位于点C左侧时,CD=DE-CE;当点D位于点C右侧时,CD=DE+CE.
解答 解:作AD⊥CD,垂足为E,
∵等腰Rt△ABC中,AC=BC,AB=2,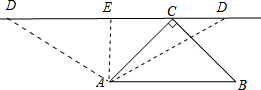
∴AE=1,
∵AD=AB=2,
∴DE=$\sqrt{3}$,
当点D位于点C左侧时,CD=DE-CE=$\sqrt{3}$-1;
当点D位于点C右侧时,CD=DE+CE=$\sqrt{3}$+1.
故答案为:$\sqrt{3}$+1或$\sqrt{3}$-1.
点评 本题主要考查了旋转的性质、勾股定理以及等腰直角三角形的性质,通过画出图形,进行分类讨论,全面的思考问题是解决问题的关键.

练习册系列答案
相关题目
8.下列结论中,正确的是( )
| A. | 圆的切线必垂直于半径 | B. | 垂直于切线的直线必经过圆心 | ||
| C. | 垂直于切线的直线必经过切点 | D. | 圆的切线垂直于经过切点的半径 |
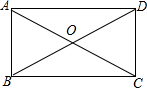 如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4.
如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4.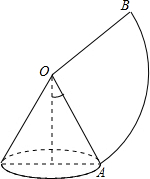 如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12.
如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12.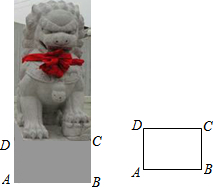 如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺.
如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺.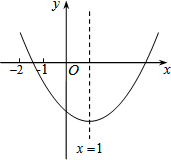 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论: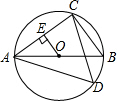 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.