题目内容
设⊙O的半径为r,圆心O到直线l的距离为d,且r,d都是关于x的一元二次方程x2-2
x+m-2=0的实数根.求当圆与直线相切时,m的值?
| 2 |
考点:直线与圆的位置关系,根的判别式
专题:常规题型
分析:根据直线与圆的位置关系得到圆与直线相切时r=d,则根据判别式的意义得到∴△=(-2
)2-4(m-2)=0,然后解关于m的一次方程即可.
| 2 |
解答:解:∵圆与直线相切,
∴r=d,
∴△=(-2
)2-4(m-2)=0,
解得m=4,
即当圆与直线相切时,m的值为4.
∴r=d,
∴△=(-2
| 2 |
解得m=4,
即当圆与直线相切时,m的值为4.
点评:本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了根的判别式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.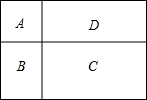 某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?
某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?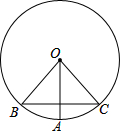 如图,在⊙O中,OA⊥BC于G,已知BC=2,OA=2,则∠BOA=
如图,在⊙O中,OA⊥BC于G,已知BC=2,OA=2,则∠BOA=