题目内容
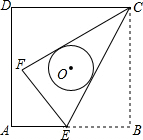 如图,正方形ABCD的边长为8,点E是AB边上的一点,将△BCE沿着CE折叠至△FCE,若CF、CE恰好与正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为8,点E是AB边上的一点,将△BCE沿着CE折叠至△FCE,若CF、CE恰好与正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )| A、10 | ||||
B、8
| ||||
C、
| ||||
| D、以上都不对 |
考点:切线的性质,正方形的性质,翻折变换(折叠问题)
专题:
分析:连接OC,则根据正方形的性质可推出∠ECF=∠BCE=
∠BCD=30°,在RT△BCE中,设BE=x,则CE=2x,利用勾股定理可得出x的值,即可得出CE的长度.
| 1 |
| 3 |
解答:解:连接OC,则∠DCO=∠BCO,∠FCO=∠ECO,
∴∠DCO-∠FCO=∠BCO-∠ECO,即∠DCF=∠BCE,
又∵△BCE沿着CE折叠至△FCE,
∴∠BCE=∠ECF,
∴∠ECF=∠BCE=
∠BCD=30°,
在RT△BCE中,设BE=x,则CE=2x,
得CE2=BC2+BE2,即4x2=x2+82,
解得BE=
,
∴CE=2x=
.
故选C.
∴∠DCO-∠FCO=∠BCO-∠ECO,即∠DCF=∠BCE,
又∵△BCE沿着CE折叠至△FCE,
∴∠BCE=∠ECF,
∴∠ECF=∠BCE=
| 1 |
| 3 |
在RT△BCE中,设BE=x,则CE=2x,
得CE2=BC2+BE2,即4x2=x2+82,
解得BE=
8
| ||
| 3 |
∴CE=2x=
16
| ||
| 3 |
故选C.
点评:此题考查了翻折变换的知识,解答本题的关键是根据切线的性质得到∠BCE=∠ECF=∠DCF=
∠BCD=30°,有一定难度.
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知图中的两个三角形全等,则∠1等于( )
已知图中的两个三角形全等,则∠1等于( )| A、70° | B、68° |
| C、58° | D、52° |
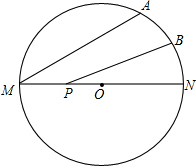 如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )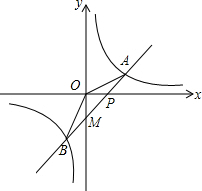 如图,一次函数y=kx-1的图象和反比例函数y=
如图,一次函数y=kx-1的图象和反比例函数y=