题目内容
 如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积.
如图,同心圆O,大圆的面积被小圆所平分,若大圆的弦AB,CD分别切小圆于E、F点,当大圆半径为R时,且AB∥CD,求阴影部分面积.考点:切线的性质,扇形面积的计算
专题:计算题
分析:连结OC、OD、OE、OF,如图,根据切线的性质得OF⊥CD,OE⊥AB,而AB∥CD,则OF⊥AB,所以EF为小圆的直径,S弓形CD=S弓形AB,再利用大圆的面积被小圆所平分,可计算OF=
R,在Rt△OCF中利用勾股定理计算出CF=
R,于是可判断△OCF为等腰直角三角形,得到∠COF=45°,所以∠COD=90°,然后根据扇形面积公式和S弓形CD=S扇形COD-S△COD计算出S弓形CD=S的面积,再利用阴影部分面积=
S大圆-2•S弓形CD进行计算.
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:解: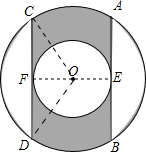 连结OC、OD、OE、OF,如图,
连结OC、OD、OE、OF,如图,
∵大圆的弦AB,CD分别切小圆于E、F点,
∴OF⊥CD,OE⊥AB,
∵AB∥CD,
∴OF⊥AB,
∴EF为小圆的直径,
∴S弓形CD=S弓形AB,
∵大圆的面积被小圆所平分,
∴π•OF2=
•πR2,
∴OF=
R,
在Rt△OCF中,∵OF=
R,OC=R,
∴CF=
=
R,
∴CD=2CF=
R,
∴OF=CF,
∴△OCF为等腰直角三角形,
∴∠COF=45°,
∴∠COD=90°,
∴S弓形CD=S扇形COD-S△COD=
-
•
R•
R=(
π-
)R2,
∴阴影部分面积=
S大圆-2•S弓形CD=
•πR2-2•(
π-
)R2=R2.
 连结OC、OD、OE、OF,如图,
连结OC、OD、OE、OF,如图,∵大圆的弦AB,CD分别切小圆于E、F点,
∴OF⊥CD,OE⊥AB,
∵AB∥CD,
∴OF⊥AB,
∴EF为小圆的直径,
∴S弓形CD=S弓形AB,
∵大圆的面积被小圆所平分,
∴π•OF2=
| 1 |
| 2 |
∴OF=
| ||
| 2 |
在Rt△OCF中,∵OF=
| ||
| 2 |
∴CF=
| OC2-OF2 |
| ||
| 2 |
∴CD=2CF=
| 2 |
∴OF=CF,
∴△OCF为等腰直角三角形,
∴∠COF=45°,
∴∠COD=90°,
∴S弓形CD=S扇形COD-S△COD=
| 90•π•R2 |
| 360 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴阴影部分面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了扇形面积得计算.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
