题目内容
如图，在△ABC中，∠C=60°，AD⊥BC于D，BE⊥AC于E．试说明△CDE∽△CBA．考点：相似三角形的判定
专题：
分析：由在△ABC中，∠C=60°，AD⊥BC于D，BE⊥AC于E．易得CE：CB=CD：CA=1：2，又由∠C是公共角，即可证得△CDE∽△CBA．
解答：证明：∵在△ABC中，∠C=60°，AD⊥BC于D，BE⊥AC于E，
∴∠CAD=∠CBE，
∴CE：CB=CD：CA=1：2，
∵∠C是公共角，
∴△CDE∽△CBA．
∴∠CAD=∠CBE，
∴CE：CB=CD：CA=1：2，
∵∠C是公共角，
∴△CDE∽△CBA．
点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
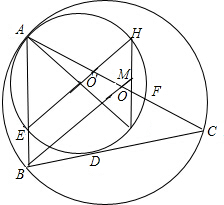已知⊙O与⊙O′内切于点A，⊙O的弦BC与⊙O′切于点D，AB、AC与⊙O′分别交于点E、F，AG、EH为⊙O′直径，BO延长线交GH于点M．
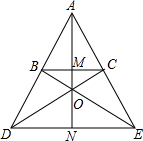如图，BC∥DE，BE与DC交于点O，AO⊥DE，垂足为N，AO交BC于点M，已知3AM=4MN，求
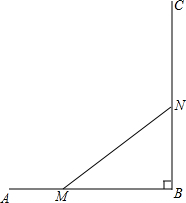如图，AB⊥BC，AB=10cm，点M以每秒1cm的速度从A开始沿AB边向点B移动，点N以每秒2cm的速度从点B开始沿BC边向点C运动，求使△MBN的面积等于24cm2时，点M运动的时间．
如图，直线AB和直线一点P，求作：