题目内容
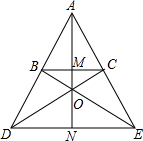如图，BC∥DE，BE与DC交于点O，AO⊥DE，垂足为N，AO交BC于点M，已知3AM=4MN，求| OM |
| ON |
考点：相似三角形的判定与性质
专题：
分析：由BC∥DE可得
=
，且∠OBC=∠OED，∠OCB=∠ODE，所以△BOC∽△EOD，AO⊥DE，所以OM和ON分别为两相似三角形对应边上的高，再结合3AM=4MN可求出相似比，即可求得对应高的比．
| AM |
| AN |
| BC |
| DE |
解答：解：∵BC∥DE，
∴
=
，且∠OBC=∠OED，∠OCB=∠ODE，
∴△BOC∽△EOD，
∵AO⊥DE，
∴OM和ON分别为两相似三角形对应边上的高，
∴
=
=
，
∵3AM=4MN，
∴
=
，
∴
=
，
∴
=
．
∴
| AM |
| AN |
| BC |
| DE |
∴△BOC∽△EOD，
∵AO⊥DE，
∴OM和ON分别为两相似三角形对应边上的高，
∴
| OM |
| ON |
| BC |
| DE |
| AM |
| AN |
∵3AM=4MN，
∴
| AM |
| MN |
| 4 |
| 3 |
∴
| AM |
| AN |
| 4 |
| 7 |
∴
| OM |
| ON |
| 4 |
| 7 |
点评：本题主要考查三角形的判定和性质，注意利用相似三角形对应边上的高的比相似比．
练习册系列答案
相关题目
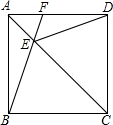在正方形ABCD中，AC为对角线，E为AC上一点，连接B、E和D、E．
下图是由小正方体搭成的立体图形，画出它的三视图．
如图，在△ABC中，∠C=60°，AD⊥BC于D，BE⊥AC于E．试说明△CDE∽△CBA．