题目内容
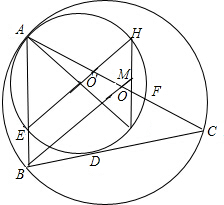 已知⊙O与⊙O′内切于点A,⊙O的弦BC与⊙O′切于点D,AB、AC与⊙O′分别交于点E、F,AG、EH为⊙O′直径,BO延长线交GH于点M.
已知⊙O与⊙O′内切于点A,⊙O的弦BC与⊙O′切于点D,AB、AC与⊙O′分别交于点E、F,AG、EH为⊙O′直径,BO延长线交GH于点M.(1)证明:BEHM为平行四边形;
(2)若AF=3,HM=1,求DE的长.
考点:圆的综合题,平行四边形的判定与性质,圆心角、弧、弦的关系,圆周角定理,圆内接四边形的性质,弦切角定理,相切两圆的性质,相似三角形的判定与性质
专题:综合题
分析:(1)由⊙O与⊙O′内切于点A可得到点O、O′、A共线,进而可证到∠AEO′=∠EAO′=∠ABO,则有EH∥BM;易证∠AEH=∠AGH=∠O′HG,则有AB∥GH,就可证到BEHM为平行四边形.
(2)过点A作两圆的公切线PQ,连接AD、DF,根据弦切角定理可得∠ABC=∠PAC=∠ADF,由圆内接四边形的性质可得∠BED=∠AFD,从而证到△BED∽△DFA,则有
=
,∠BDE=∠DAF.根据弦切角定理可得∠BDE=∠EAD,从而有∠EAD=∠DAF,进而可得到DE=DF.由BEHM为平行四边形可得BE=MH=1,把FA=3,BE=1,DE=DF代入
=
就可求出ED的长.
(2)过点A作两圆的公切线PQ,连接AD、DF,根据弦切角定理可得∠ABC=∠PAC=∠ADF,由圆内接四边形的性质可得∠BED=∠AFD,从而证到△BED∽△DFA,则有
| ED |
| FA |
| BE |
| DF |
| ED |
| FA |
| BE |
| DF |
解答:(1)证明:∵⊙O与⊙O′内切于点A,
∴点O、O′、A共线.
∵O′A=O′E,OA=OB,
∴∠AEO′=∠EAO′=∠ABO.
∴EH∥BM.
∵O′G=O′H,∴∠O′HG=∠O′GH.
∵∠AEH=∠AGH,∴∠AEH=∠O′HG.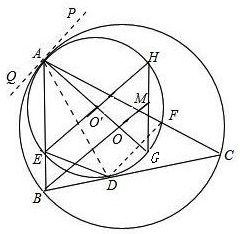
∴AB∥GH.
∴BEHM为平行四边形.
(2)解:过点A作两圆的公切线PQ,连接AD、DF,如图所示.
则根据弦切角定理可得:∠ABC=∠PAC,∠PAF=∠ADF.
∴∠ABC=∠ADF.
由圆内接四边形的性质可得:∠BED=∠AFD.
∴△BED∽△DFA.
∴
=
,∠BDE=∠DAF.
∵BC与⊙O′切于点D,
∴根据弦切角定理可得:∠BDE=∠EAD.
∴∠EAD=∠DAF.
∴
=
.
∴DE=DF.
∵BEHM为平行四边形,∴BE=MH.
∵AF=3,BE=HM=1,
∴
=
.
解得:DE=
.
∴DE的长为
.
∴点O、O′、A共线.
∵O′A=O′E,OA=OB,
∴∠AEO′=∠EAO′=∠ABO.
∴EH∥BM.
∵O′G=O′H,∴∠O′HG=∠O′GH.
∵∠AEH=∠AGH,∴∠AEH=∠O′HG.

∴AB∥GH.
∴BEHM为平行四边形.
(2)解:过点A作两圆的公切线PQ,连接AD、DF,如图所示.
则根据弦切角定理可得:∠ABC=∠PAC,∠PAF=∠ADF.
∴∠ABC=∠ADF.
由圆内接四边形的性质可得:∠BED=∠AFD.
∴△BED∽△DFA.
∴
| ED |
| FA |
| BE |
| DF |
∵BC与⊙O′切于点D,
∴根据弦切角定理可得:∠BDE=∠EAD.
∴∠EAD=∠DAF.
∴
 |
| DE |
 |
| DF |
∴DE=DF.
∵BEHM为平行四边形,∴BE=MH.
∵AF=3,BE=HM=1,
∴
| ED |
| 3 |
| 1 |
| DE |
解得:DE=
| 3 |
∴DE的长为
| 3 |
点评:本题主要考查了相切两圆的性质、弦切角定理、圆周角定理、弧与弦的关系、圆内接四边形的性质、平行四边形的判定与性质、相似三角形的判定与性质、等腰三角形的性质、平行线的判定等知识,综合性比较强.而作相切两圆的公切线,并根据弦切角定理得到角等是解决第(2)小题的关键.

练习册系列答案
相关题目
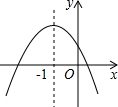 已知二次函数y=ax2+bx+c的图象如图,下列结论:①a+b+c<0;②△<0;③abc<0; ④b=2a;⑤a-b+c>0,正确的个数是( )
已知二次函数y=ax2+bx+c的图象如图,下列结论:①a+b+c<0;②△<0;③abc<0; ④b=2a;⑤a-b+c>0,正确的个数是( )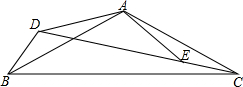 在△ABC中,AB=25,BC=40,AC=20,在△ADE中,AE=12,AD=15,DE=24,求证:△ADB∽△AEC.
在△ABC中,AB=25,BC=40,AC=20,在△ADE中,AE=12,AD=15,DE=24,求证:△ADB∽△AEC.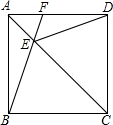 在正方形ABCD中,AC为对角线,E为AC上一点,连接B、E和D、E.
在正方形ABCD中,AC为对角线,E为AC上一点,连接B、E和D、E. 如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E.试说明△CDE∽△CBA.
如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E.试说明△CDE∽△CBA.