题目内容
在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tanA+tanB的值为 .

3
考点: 锐角三角函数的定义.
分析: 由△ABC的面积为6可得ab=12,再由勾股定理可得a2+b2=62=36,再由tanA+tanB= +
+ =
= 求解.
求解.
解答: 解:∵△ABC的面积为6,
∴ab=12.
在Rt△ABC中,∠C=90°,AB=6,
∴a2+b2=62=36,
∴tanA+tanB=
 =
= =
= =3,
=3,
故答案为:3.
点评: 本题考查锐角三角函数的概念和勾股定理,关键是掌握正切定义.

练习册系列答案
相关题目
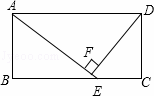

 )米 B. 12米 C. (
)米 B. 12米 C. (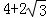 )米 D. 10米
)米 D. 10米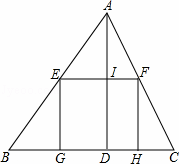
 cm C. 5πcm D. 5
cm C. 5πcm D. 5 )÷(﹣1
)÷(﹣1 )+(﹣2)2×(﹣3)
)+(﹣2)2×(﹣3)