题目内容
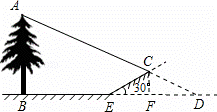
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )

A. ( )米 B. 12米 C. (
)米 B. 12米 C. (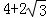 )米 D. 10米
)米 D. 10米
A
考点: 解直角三角形的应用-坡度坡角问题.
分析: 延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.
解答: 解:延长AC交BF延长线于D点,
则∠CEF=30°,作CF⊥BD于F,
在Rt△CEF中,∠CEF=30°,CE=4m,
∴CF=2(米),EF=4cos30°=2 (米),
(米),
在Rt△CFD中,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,
即CF=2(米),CF:DF=1:2,
∴DF=4(米),
∴BD=BE+EF+FD=12+2 (米)
(米)
在Rt△ABD中,AB=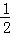 BD=
BD=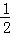 (12+2
(12+2 )=(
)=( +6)米.
+6)米.
故选A.
点评: 本题考查了解直角三角形的应用以及相似三角形的性质.解决本题的关键是作出辅助线得到AB的影长.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 .
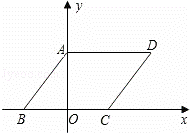
.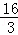 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?