题目内容
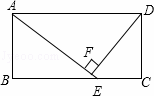
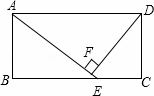
如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
考点: 相似三角形的判定与性质;勾股定理;矩形的性质.
专题: 几何综合题.
分析: (1)根据矩形的性质和DF⊥AE,可得∠ABE=∠AFD=90°,∠AEB=∠DAF,即可证明△ABE∽△DFA.
(2)利用△ABE∽△ADF,得 =
= ,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
解答: 解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴ =
= ,
,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF=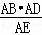 =
=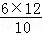 =7.2.
=7.2.
答:DF的长为7.2.
点评: 此题主要考查学生对相似三角形的判定与性质、勾股定理和矩形的性质的理解和掌握,难度不大,属于基础题.

练习册系列答案
相关题目


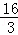 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?