题目内容
育英中学举行秋季运动会,王建同学参加铅球比赛,铅球出手时距地面1.6m,当铅球达到最大高度1.96m时水平方向距王建3m,若前一位选手成绩为9.9m,那么王建 (“能”或“不能”)超过他,成绩为 m.(设铅球在空中飞行路线呈抛物线)
考点:二次函数的应用,二次函数的最值
专题:
分析:先建立平面直角坐标系,已知抛物线上的B,C两点,其中C(3,1.96)为顶点坐标,可设顶点式,再代入B点求得a,从而求得解析式,再求出OD的长,可得问题答案.
解答: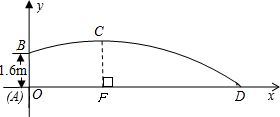 解:建立如图所示的平面直角坐标系,
解:建立如图所示的平面直角坐标系,
由题意得B(0,1.6)、C(3,1.96),
设抛物线解析式y=a(x-3)2+1.96.
将B(0,1.6)代入,得a(0-3)2+1.96=1.6,
解得a=-0.04,
∴抛物线解析式y=-0.04(x-3)2+1.96,
设D(x,0)代入,得-0.04(x-3)2+1.96=0,
解得x=10或-4(负值舍去),
∴x=10(米),
10米>9.9米,
∴王建能超过,他的成绩为10米,
故答案为:能;10.
 解:建立如图所示的平面直角坐标系,
解:建立如图所示的平面直角坐标系,由题意得B(0,1.6)、C(3,1.96),
设抛物线解析式y=a(x-3)2+1.96.
将B(0,1.6)代入,得a(0-3)2+1.96=1.6,
解得a=-0.04,
∴抛物线解析式y=-0.04(x-3)2+1.96,
设D(x,0)代入,得-0.04(x-3)2+1.96=0,
解得x=10或-4(负值舍去),
∴x=10(米),
10米>9.9米,
∴王建能超过,他的成绩为10米,
故答案为:能;10.
点评:本题主要考查二次函数的应用,由函数图象写出函数解析式,用二次函数解决实际问题,比较简单.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
二次函数y=x2-4x+3的图象的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
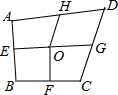 小李家有一块四边形菜地ABCD,这块菜地里有一口井O,从O向四边的中点挖了四条水渠,分别是OE,OF,OG,OH,把四边形菜地分成四块(如图所示),已知四边形AEOH的面积等于30 m2,四边形EOFB的面积为40 m2,四边形OFCG的面积为50 m2,那么请你算一算四边形DGOH的面积是
小李家有一块四边形菜地ABCD,这块菜地里有一口井O,从O向四边的中点挖了四条水渠,分别是OE,OF,OG,OH,把四边形菜地分成四块(如图所示),已知四边形AEOH的面积等于30 m2,四边形EOFB的面积为40 m2,四边形OFCG的面积为50 m2,那么请你算一算四边形DGOH的面积是 实验探究:为发挥广大读者艺术特长,我报《数学专页》于2006年1月份举办了一次栏标设计大赛,截至4月份大赛已圆满结束.本次比赛收到了近千幅设计作品,其中一幅参赛作品如图.
实验探究:为发挥广大读者艺术特长,我报《数学专页》于2006年1月份举办了一次栏标设计大赛,截至4月份大赛已圆满结束.本次比赛收到了近千幅设计作品,其中一幅参赛作品如图.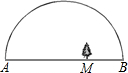 方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.
方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米. 图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有
图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有 如图,在△ABC中,∠A=40°,∠B=65°,则∠C=
如图,在△ABC中,∠A=40°,∠B=65°,则∠C=