题目内容
10.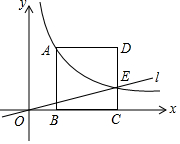 如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )
如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )| A. | $\frac{9}{2}$ | B. | 5 | C. | $\frac{2}{9}$ | D. | 3 |
分析 根据A点坐标求出B点坐标及C点坐标,再用m表示出E点坐标,根据反比例函数图象上点的坐标特点求出m的值,进而可得出结论.
解答 解:∵点A(m,m+3),
∴B(m,0),C(2m+3).
∵OB-CE=1,
∴E(2m+3,m-1).
∵AE两点在同一个反比例函数的图象上,
∴m(m+3)=(2m+3)(m-1),解得m1=-1(舍去),m2=3,
∴E(9,2),
∴tan∠EOC=$\frac{CE}{OC}$=$\frac{2}{9}$.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.在实数0、π、$\frac{22}{7}$、$\sqrt{3}$、-$\sqrt{9}$中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.当x=-6,y=$\frac{1}{6}$时,x2016y2017的值为( )
| A. | -6 | B. | 6 | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
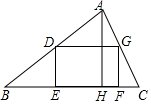 如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.
如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36. 如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,做直线MN交AB于点D,连接CD,若AB=6,AC=4,则△ACD的周长为( )
如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,做直线MN交AB于点D,连接CD,若AB=6,AC=4,则△ACD的周长为( )