题目内容
5．计算：$\sqrt{（2-\sqrt{3}）^{2}}$+$\sqrt{（\sqrt{3}-1）^{2}}$=1．分析 根据$\sqrt{{a}^{2}}$=|a|，再利用绝对值的性质去绝对值合并同类二次根式进行计算即可．
解答 解：原式=|2-$\sqrt{3}$|+|$\sqrt{3}-1$|=2$-\sqrt{3}$+$\sqrt{3}-1$=1，
故答案为：1．
点评 此题主要考查了二次根式的性质和计算，关键是掌握$\sqrt{{a}^{2}}$=|a|．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
16．下列多项式中，不能运用公式法因式分解的是（ ）
| A． | 9a2-3a+1 | B． | a2-16b2 | C． | a${\;}^{2}+\frac{1}{4}{b}^{2}+ab$ | D． | （x+y）2-4（x+y）+4 |
13．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （a2）3=a5 | C． | （3a）2=9a2 | D． | a6÷a3=a2 |
20．下列计算正确的是（ ）
| A． | $\sqrt{9}$=±3 | B． | -$\root{3}{64}$=-4 | C． | $\sqrt{{{（-0.2）}^2}}$=-0.2 | D． | ±$\sqrt{\frac{16}{49}}$=$\frac{4}{7}$ |
10．
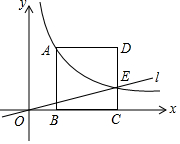如图所示，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象经过顶点A（m，m+3）和CD上的点E，且OB-CE=1．直线l过O、E两点，则tan∠EOC的值为（ ）
如图所示，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象经过顶点A（m，m+3）和CD上的点E，且OB-CE=1．直线l过O、E两点，则tan∠EOC的值为（ ）| A． | $\frac{9}{2}$ | B． | 5 | C． | $\frac{2}{9}$ | D． | 3 |