题目内容
5.甲、乙、丙三名学生竞选学生会主席,他们的笔试、面试成绩如下统计表和统计图竞选的最后一道程序是由 200名学生代表名候选人投票,每人只能投一票(不设弃权票),三名候选人投票结果如统计图2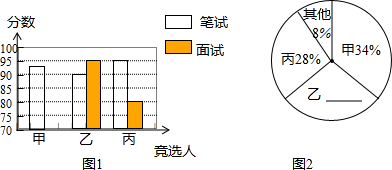
| 测试 项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)补全图1和图2;
(2)请直接写出每名候选人的得票数;
(3)学校规定:候选人每得一票记1分,并将笔试、面试、投票三项得分按5:3:2的比例确定个人成绩,请计算三名候选人的最后成绩,并根据成绩判断谁能当选.
分析 (1)结合图表和扇形统计图所给的数据,即可得出答案,从而补全统计图;
(2)根据甲、乙、丙所占的百分比和总人数,即可得出每名候选人的得票数;
(3)根据加权平均数的计算公式先求出甲、乙、丙的平均数,再进行比较即可.
解答  解:(1)根据图表可得:甲的面试是85分,
解:(1)根据图表可得:甲的面试是85分,
乙所占的百分比是1-8%-34%-28%=30%,
补图如右:
(2)甲的得票数是:200×34%=68(票),
乙的得票数是:200×30%=60(票),
丙的得票数是:200×28%=56(票);
(3)∵$\overline{{x}_{甲}}$=$\frac{92×5+85×3+68×2}{10}$=85.1(分),
$\overline{{x}_{乙}}$=$\frac{90×5+95×3+60×2}{10}$=85.5(分),
$\overline{{x}_{丙}}$=$\frac{95×5+80×3+56×2}{10}$=82.7(分),
∴乙的最后成绩最高,
∴乙能当选.
点评 此题考查了条形统计图、扇形统计图与加权平均数,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.抛物线y=$\frac{1}{2}$(x-1)2+2的顶点坐标为( )
| A. | (-1,2) | B. | (-1,-2) | C. | (1,2) | D. | (1,-2) |
13.下列各式中,运算正确的是( )
| A. | 2x2-x=x2 | B. | (x2)3=x5 | C. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | D. | x2•x3=x6 |
20.某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了3782张相片.若全班有x名学生,根据题意,列出方程为( )
| A. | x(x-1)=3782 | B. | $\frac{x(x-1)}{2}$=3782 | C. | 2x(x-1)=3782 | D. | x(x+1)=3782 |
10.在平面直角坐标系中,反比例函数y=$\frac{{a}^{2}-a+1}{x}$图象的两个分支分别在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、四象限 | D. | 第一、三象限 |
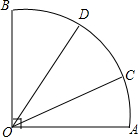 如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.
如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.