题目内容
利用配方法,求代数式4m2-2m+7的最小值.
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:先将原式变形为4m2-2m+7=4(m-
)2+
,由非负数的性质就可以求出最小值.
| 1 |
| 4 |
| 27 |
| 4 |
解答:解:原式=4(m2-
m)+7
=4(m-
)2+
,
∵(m-
)2≥0,
∴(m-
)2+
的最小值是
.
| 1 |
| 2 |
=4(m-
| 1 |
| 4 |
| 27 |
| 4 |
∵(m-
| 1 |
| 4 |
∴(m-
| 1 |
| 4 |
| 27 |
| 4 |
| 27 |
| 4 |
点评:本题考查了配方法的运用,非负数的性质,一个数的偶次幂为非负数的运用.解答时配成完全平方式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各组中的两个单项式不是同类项的是( )
| A、2a3b与-ba3 | ||||
| B、-3与0 | ||||
C、
| ||||
| D、6a2m与-9a2m |
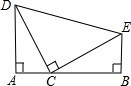 已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE.
已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE. 养鸡专业户计划用116m的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽各为1m,怎样设计才能使围成的鸡舍面积最大?
养鸡专业户计划用116m的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽各为1m,怎样设计才能使围成的鸡舍面积最大?