题目内容
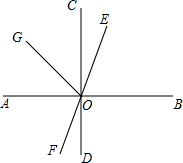如图，直线AB，CD，EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=28°，求：∠BOE和∠AOG的度数．考点：垂线,对顶角、邻补角
专题：
分析：先根据对顶角相等求出∠COE=∠FOD，得出∠BOE，再根据邻补角求出∠AOE，由角平分线即可求出∠AOG．
解答：
解：∵AB⊥CD，
∴∠BOC=90°，
∵∠COE=∠FOD=28°，
∴∠BOE=90°-∠28°=62°，
∴∠AOE=180°-∠BOE=118°，
∵OG平分∠AOE，
∴∠AOG=
∠AOE=59°．
∴∠BOC=90°，
∵∠COE=∠FOD=28°，
∴∠BOE=90°-∠28°=62°，
∴∠AOE=180°-∠BOE=118°，
∵OG平分∠AOE，
∴∠AOG=
| 1 |
| 2 |
点评：本题考查了垂线、对顶角、邻补角的定义；弄清各个角之间的数量关系是解决问题的关键．
练习册系列答案
相关题目
下列各式中是单项式的是（ ）
A、-
| ||
B、
| ||
| C、0 | ||
D、
|
单项式-3x2y的系数和次数分别是（ ）
| A、-3和2 | B、3和-3 |
| C、-3和3 | D、3和2 |
有理数a、b在数轴上的对应位置如图所示，下列结论正确的是（ ）| A、a+b＞0 |
| B、a-b＞0 |
| C、|a+b|＞|a-b| |
| D、a-（-a+b）＜0 |