题目内容
已知(a-2)2+(b+2)2+(c-3)2=0,求
a2b3c4•(3ab2c2)2÷6(a2b3c4)2的值.
| 1 |
| 3 |
考点:整式的混合运算—化简求值,非负数的性质:偶次方
专题:计算题
分析:利用非负数的性质求出a,b,c的值,原式先计算乘方运算,再计算乘除运算,即可得到结果.
解答:
解:∵(a-2)2+(b+2)2+(c-3)2=0,
∴a=2,b=-2,c=3,
则原式=
a2b3c4•(9a2b4c4)÷6(a4b6c8)=
.
∴a=2,b=-2,c=3,
则原式=
| 1 |
| 3 |
| 1 |
| 2 |
点评:此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
已知m+n=5,n-m=3,则n2-m2等于( )
| A、5 | B、15 | C、25 | D、9 |
若关于x的不等式
的解集为x<2,则a的取值范围是( )
|
| A、a>-2 | B、a≥-2 |
| C、a≤-2 | D、a<-2 |
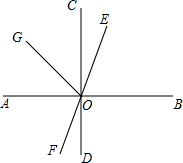 如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求:∠BOE和∠AOG的度数.
如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求:∠BOE和∠AOG的度数.