题目内容
已知关于x的一元二次方程ax2+bx+m=0中.(a-m)2+(b-m-1)2=0
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相同的实数根,求方程的根.
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相同的实数根,求方程的根.
考点:根的判别式,解一元二次方程-配方法
专题:
分析:(1)由条件(a-m)2+(b-m-1)2=0可得a=m,b=m+1,然后根据a=4即可求出m、b的值;
(2)根据条件可得b2-4a=0,然后把a=m,b=m+1代入b2-4a=0,即可求出m的值,从而得到a、b的值,然后解原方程即可.
(2)根据条件可得b2-4a=0,然后把a=m,b=m+1代入b2-4a=0,即可求出m的值,从而得到a、b的值,然后解原方程即可.
解答:解:(1)∵(a-m)2+(b-m-1)2=0
∴a-m=0,b-m-1=0,
∴a=m,b=m+1.
∵a=4,
∴m=4,
∴b=5;
(2)∵方程ax2+bx+1=0有两个相同的实数根,
∴b2-4a=0.
∵a=m,b=m+1,
∴(m+1)2-4m=0
解得:m1=m2=1,
∴a=1,b=2,
∴原方程为x2+2x+1=0,
解得:x1=x2=-1.
∴a-m=0,b-m-1=0,
∴a=m,b=m+1.
∵a=4,
∴m=4,
∴b=5;
(2)∵方程ax2+bx+1=0有两个相同的实数根,
∴b2-4a=0.
∵a=m,b=m+1,
∴(m+1)2-4m=0
解得:m1=m2=1,
∴a=1,b=2,
∴原方程为x2+2x+1=0,
解得:x1=x2=-1.
点评:本题主要考查了非负数的性质、根的判别式、解一元二次方程等知识,运用根的判别式是解决本题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
2013年11月9日是国人的骄傲的日子,有约1.2亿中国人关注了广州恒大队与韩国首尔FC队的亚洲冠军杯决赛,最终广州恒大队不负众望夺取冠军,其中1.2亿用科学记数法可表示为( )
| A、12×108 |
| B、1.28 |
| C、0.12×109 |
| D、1.2×108 |
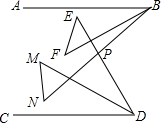 如图,AB∥CD,求∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM的度数是
如图,AB∥CD,求∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM的度数是 如图,正比例函数y=kx与反比例函数y=-
如图,正比例函数y=kx与反比例函数y=-
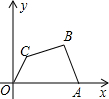 如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).
如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).