题目内容
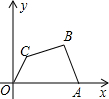 如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).
如图,在平面直角坐标系中,点A、B、C的坐标分别为A(5,0),B(4,3),C(1,2).(1)求直线OC所表达的函数关系式;
(2)求图中四边形OABC的面积.
考点:待定系数法求一次函数解析式
专题:
分析:(1)设OC的表达式y=kx,把C(1,2)代入即可得出k的值;
(2)过点C、B分别作CD⊥OA,BE⊥OA,把四边形OABC的面积分成△OCD、四边形BCDE、△ABE的面积,求解即可.
(2)过点C、B分别作CD⊥OA,BE⊥OA,把四边形OABC的面积分成△OCD、四边形BCDE、△ABE的面积,求解即可.
解答: 解:(1)设OC的表达式y=kx,把C(1,2)代入y=kx得,k=2,
解:(1)设OC的表达式y=kx,把C(1,2)代入y=kx得,k=2,
∴直线OC所表达的函数关系式y=2x;
(2)过点C、B分别作CD⊥OA,BE⊥OA,垂直为D,E,
∵A(5,0),B(4,3),C(1,2),
∵S四边形OABC=S△OCD+S四边形BCDE+S△ABE
=
×1×2+
×(2+3)×3+
×1×3
=1+7.5+1.5
=10.
 解:(1)设OC的表达式y=kx,把C(1,2)代入y=kx得,k=2,
解:(1)设OC的表达式y=kx,把C(1,2)代入y=kx得,k=2,∴直线OC所表达的函数关系式y=2x;
(2)过点C、B分别作CD⊥OA,BE⊥OA,垂直为D,E,
∵A(5,0),B(4,3),C(1,2),
∵S四边形OABC=S△OCD+S四边形BCDE+S△ABE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+7.5+1.5
=10.
点评:本题考查了用待定系数法求一次函数的解析式,以及四边形的面积,把四边形的面积分为三角形的面积和梯形的面积是解题的关键.

练习册系列答案
相关题目
下面的每组图形中,左面的平移后可以得到右面的是( )
A、 |
B、 |
C、 |
D、 |
下列不是平移现象的是( )
| A、站在运行着电梯上的人 |
| B、小刘荡秋千的运动 |
| C、左右推动的窗户 |
| D、躺在火车上睡觉的人 |
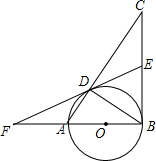 如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F. 如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论.
如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论. 如图,四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,AD=5,求等腰梯形ABCD的周长.
如图,四边形ABCD是等腰梯形,BC∥AD,AB=DC,BD⊥CD,AC⊥AB,∠BAD=120°,AD=5,求等腰梯形ABCD的周长.