题目内容
观察下列不等式:
=
(1-
),
=
(
-
),
=
(
-
),
=
(
-
)…
根据以上式子的规律,填空
= .
| 1 |
| 1×2×4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2×3×4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4×4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5×4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
根据以上式子的规律,填空
| 1 |
| n×(n+1)×4 |
考点:规律型:数字的变化类
专题:
分析:由等式可以看出:分子是1,分母是连续两个自然数的乘积再乘4,结果等于分子是1,分母是这两个自然数的分数差再乘
,由此规律得出答案即可.
| 1 |
| 4 |
解答:解:∵
=
(1-
),
=
(
-
),
=
(
-
),
=
(
-
)
…
∴
=
(
-
).
故答案为:
(
-
).
| 1 |
| 1×2×4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2×3×4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4×4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5×4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
…
∴
| 1 |
| n×(n+1)×4 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
故答案为:
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
已知太阳的半径约为696000000m,则696000000这个数用科学记数法可表示为( )
| A、0.696×109 |
| B、6.96×109 |
| C、6.96×108 |
| D、69.6×107 |
已知三条线段长分别为a、b、c,a<b<c(a、b、c均为整数),若c=6,则线段a、b、c能组成三角形的情形有( )
| A、3种 | B、4种 | C、5种 | D、6种 |
下面的每组图形中,左面的平移后可以得到右面的是( )
A、 |
B、 |
C、 |
D、 |
 在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器水面高度h与时间t的函数图象如图所示,那么这个容器的形状可能是( )
在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器水面高度h与时间t的函数图象如图所示,那么这个容器的形状可能是( )



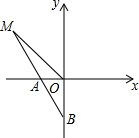 如图,M(m,n)为第二象限内一点,且m,n恰好为方程t2+2t+p=0的两个根,M点与原点的距离为2
如图,M(m,n)为第二象限内一点,且m,n恰好为方程t2+2t+p=0的两个根,M点与原点的距离为2