题目内容
在计数制中,通常我们使用的是“十进制”,即“逢十进一”.而计数制方法很多,如60进制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7天化为1周等…,而二进制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表:
请将二进制数101001(2)写成十进制数为 .
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 二进制 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | … |
考点:有理数的混合运算
专题:新定义
分析:根据二进制与十进制的转化方法列式算式进行计算即可得解.
解答:解:二进制数101001(2)写成十进制数为:
1×25+0×24+1×23+0×22+0×21+1×20
=32+0+8+0+0+1
=41.
故答案为:41.
1×25+0×24+1×23+0×22+0×21+1×20
=32+0+8+0+0+1
=41.
故答案为:41.
点评:本题考查了有理数的运算,理解二进制的意义是关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
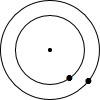 如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )
如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )A、0<
| ||
B、1<
| ||
C、2<
| ||
D、3<
|
 某数学兴趣小组在探索“圆的有关相交弦问题”时,
某数学兴趣小组在探索“圆的有关相交弦问题”时, 如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,若AB=2,AD=3,则tanB的值为
如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,若AB=2,AD=3,则tanB的值为 如图,一架长10m的梯子斜靠在一竖直的墙上,这时梯足距离墙底端6m,如果梯子向外平移2m,那么梯子的顶端将下滑
如图,一架长10m的梯子斜靠在一竖直的墙上,这时梯足距离墙底端6m,如果梯子向外平移2m,那么梯子的顶端将下滑 如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有
如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有