题目内容
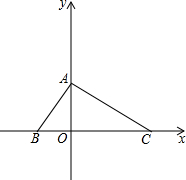 如图,在平面直角坐标系中,已知S△ABO=8,OA=OB,BC=12,点P的坐标是(a,6).
如图,在平面直角坐标系中,已知S△ABO=8,OA=OB,BC=12,点P的坐标是(a,6).(1)求△ABC三个顶点的坐标;
(2)连接PA、PB,并用含字母a的式子表示△PAB的面积;
(3)是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,求出点P的坐标.
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:(1)根据三角形面积公式得到
•OA2=8,解得OA=4,则OB=OA=4,OC=BC-OB=8,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
(2)分类讨论:当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,利用S△PAB=S△AOB+S梯形AOHP-S△PBH求解;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,利用S△PAB=S梯形OHPB-S△PAH-S△OAB求解;
(3)先计算出S△ABC=24,再根据(2)中的分类得到2a-4=24或4-2a=24,然后分别求出a的值,从而确定P点坐标.
| 1 |
| 2 |
(2)分类讨论:当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,利用S△PAB=S△AOB+S梯形AOHP-S△PBH求解;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,利用S△PAB=S梯形OHPB-S△PAH-S△OAB求解;
(3)先计算出S△ABC=24,再根据(2)中的分类得到2a-4=24或4-2a=24,然后分别求出a的值,从而确定P点坐标.
解答:解:(1)∵S△ABO=
•OA•OB,
而OA=OB,
∴
•OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BC-OB=12-4=8,
∴A(0,4),B(-4,0),C(8,0);
(2)当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,
S△PAB=S△AOB+S梯形AOHP-S△PBH=8+
•a-
•6•(a+4)=2a-4;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,
 S△PAB=S梯形OHPB-S△PAH-S△OAB=
S△PAB=S梯形OHPB-S△PAH-S△OAB=
•6-
•(6-4)•a-8=4-2a;
(3)存在.
S△ABC=
•4•12=24,
当P(a,6)在第一象限,则2a-4=24,解得a=14,此时P点坐标为(14,6);
当P(a,6)在第二象限,则4-2a=24,解得a=-10,此时P点坐标为(-10,6),
综上所述,点P的坐标为(-10,6)或(14,6).
| 1 |
| 2 |

而OA=OB,
∴
| 1 |
| 2 |
∴OB=OA=4,
∴OC=BC-OB=12-4=8,
∴A(0,4),B(-4,0),C(8,0);
(2)当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,
S△PAB=S△AOB+S梯形AOHP-S△PBH=8+
| 4+6 |
| 2 |
| 1 |
| 2 |
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,
 S△PAB=S梯形OHPB-S△PAH-S△OAB=
S△PAB=S梯形OHPB-S△PAH-S△OAB=| 4-a |
| 2 |
| 1 |
| 2 |
(3)存在.
S△ABC=
| 1 |
| 2 |
当P(a,6)在第一象限,则2a-4=24,解得a=14,此时P点坐标为(14,6);
当P(a,6)在第二象限,则4-2a=24,解得a=-10,此时P点坐标为(-10,6),
综上所述,点P的坐标为(-10,6)或(14,6).
点评:本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住三角形面积公式.

练习册系列答案
相关题目
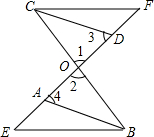 EF与BC交于点O,AB∥CD,OA=OD,AE=DF,∠1、∠2、∠3、∠4如图所示,求证:EB∥CF.
EF与BC交于点O,AB∥CD,OA=OD,AE=DF,∠1、∠2、∠3、∠4如图所示,求证:EB∥CF. 看图填空:
看图填空: (1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是:
(1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是: