题目内容
5.点P在图形M上,点Q在图形N上,记dmax(M,N)为线段PQ长度的最大值,dmin(M,N)为线段PQ长度的最小值,图形M、N的平均距离Ed(M,N)=$\frac{{{d_{max}}(M,N)+{d_{min}}(M,N)}}{2}$.已知A(0,0),B(2,0),C(4,2),线段AB以每秒1个单位的速度沿着x轴正方向匀速运动.
(1)如图1,求经过1秒后,Ed(C,AB);
(2)写出线段AB在运动过程中Ed(C,AB)关于时间t的函数解析式;
(3)如图2,已知抛物线的一部分m:y=(x-2)2+$\frac{9}{4}$(0≤x≤2)和线段EF:y=-x+1(0≤x≤1),求Ed(EF,m).
分析 (1)求出当t=1时A、B、C的坐标,再求出AC及BC的值,进而可得出结论;
(2)分t<2或t>4;2<t<3;3<t<4三种情况进行讨论;
(3)设与EF平行且与抛物线只有一个公共点的D的直线L的解析式为y=-x+b,联立两直线的解析式得出D点坐标,过点D且垂直于直线EF的解析式为y=x+1,故dmin(EF,m)=DE,dmax(EF,m)=HF,由此可得出结论.
解答 解:(1)∵当t=1时,A(1,0),B(3,0),C(4,2).
∴dmax=AC=$\sqrt{13}$,dmin=BC=$\sqrt{5}$,
∴Ed(C,AB)=$\frac{\sqrt{13}+\sqrt{5}}{2}$;
(2)依题意得 A(t,0),B(t+2,0)
当t<2或t>4时,Ed(C,AB)=$\frac{\sqrt{(4-t)^{2}+4}+\sqrt{(t-2)^{2}+4}}{2}$;
当2<t<3时,Ed(C,AB)=$\frac{\sqrt{{(4-t)}^{2}+4}+2}{2}$;
当3<t<4时,Ed(C,AB)=$\frac{2+\sqrt{{(t-2)}^{2}+4}}{2}$.
(3)如图,设与EF平行且与抛物线只有一个公共点的D的直线L的解析式为y=-x+b,
由-x+b=(x-2)2+$\frac{9}{4}$,令△=0,得b=4,即L为:y=- x+4
x+4
由又∵$\left\{\begin{array}{l}y=-x+4\\ y=(x-2)^{2}+\frac{9}{4}\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{3}{2}\\ y=\frac{5}{2}\end{array}\right.$,
∴D($\frac{3}{2}$,$\frac{5}{2}$).
过点D且垂直于直线EF的解析式为:y=x+1
∵y=x+1与y=-x+1交于点E(0,1)
∴dmin(EF,m)=DE=$\frac{3\sqrt{2}}{2}$.
又∵抛物线与y轴交于点H,
∴dmax(EF,m)=HF=$\frac{\sqrt{641}}{4}$,
∴Ed(EF,m)=$\frac{6\sqrt{2}+\sqrt{641}}{8}$.
点评 本题考查的是二次函数综合题,涉及到直线与抛物线相切与垂直的问题,解题的关键是正确理解题中最大值、最小值与平均值的表示方法.

| A. | 折线统计图 | B. | 条形统计图 | C. | 扇形统计图 | D. | 以上均可以 |
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96-x)=72-x | C. | $\frac{1}{3}$(96+x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
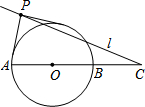 如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9. 如图,在Rt△ABC中,∠A=90°,∠B=30°,AB=6,求BC.
如图,在Rt△ABC中,∠A=90°,∠B=30°,AB=6,求BC. 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x. 如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.
如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.