题目内容
7.不等式组$\left\{\begin{array}{l}{x-3≤0}\\{3-(x-2)<7}\end{array}\right.$的解集在数轴上表示正确的是( )| A. | 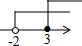 | B. |  | C. | 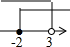 | D. | 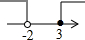 |
分析 首先解不等式组中的每个不等式,然后确定两个不等式的解集的公共部分,即可确定不等式组的解集.
解答 解:解第一个不等式得:x≤3,
解第二个不等式得:x>-2,
则不等式组的解集是:-2<x≤3.
故选:B.
点评 本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(-1,-1),(0,0),($\sqrt{2},\sqrt{2}$),…都是“梦之点”,显然,这样的“梦之点”有无数个,应用:若点P(2,m)是反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象上的“梦之点”,则这个反比例函数的解析式是( )
| A. | y=$\frac{2}{x}$ | B. | y=$\frac{2m}{x}$ | C. | y=$\frac{{m}^{2}}{x}$ | D. | y=$\frac{4}{x}$ |
12. 把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
 把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC等于( )| A. | 90° | B. | 100° | C. | 105° | D. | 120° |
17.⊙O的半径为5,同一平面内有一点P,且OP=7,则P与⊙O的位置关系是( )
| A. | P在圆内 | B. | P在圆上 | C. | P在圆外 | D. | 无法确定 |
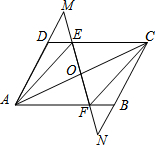 如图,平行四边形ABCD中,EF过对角线AC的中点O,且EF⊥AC交CD于E,交AB于F,分别交AD、CB的延长线于M、N.
如图,平行四边形ABCD中,EF过对角线AC的中点O,且EF⊥AC交CD于E,交AB于F,分别交AD、CB的延长线于M、N.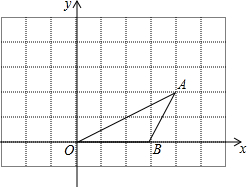 如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′.
如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′. 如图,AB是⊙O的直径,点C在⊙O上,CE⊥AB于E,CD平分∠ECB,交切线BD于D,交AB于F.
如图,AB是⊙O的直径,点C在⊙O上,CE⊥AB于E,CD平分∠ECB,交切线BD于D,交AB于F.