Question

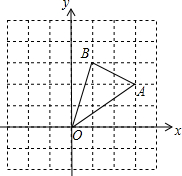如图，在边长为1的正方形组成的网格中，△△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到A₁OB₁．
（1）画出旋转后的图形；
（2）点A₁的坐标为

 

；
（3）求线段OB在旋转过程中所扫过的图形面积（写过程）．

Answer 1

考点：作图-旋转变换,扇形面积的计算

专题：

分析：（1）根据旋转的性质得出对应点位置，进而得出答案；
（2）根据所画图形得出点A₁的坐标；
（3）利用扇形面积公式进而得出线段OB在旋转过程中所扫过的图形面积．

解答：解：（1）如图所示：△A₁B₁O即为所求；

（2）点A₁的坐标为：（-2，3）；

（3）点B扫过的图形为扇形BOB₁，
∵旋转角为90°，
∴∠BOB₁=90°，
∵点B（1，3），
∴OB=

10

，
∴S_扇形BOB1=

nπr2

360

=

90π×10

360

=

5

2

π．

点评：此题主要考查了图形的旋转以及扇形面积求法，得出旋转后对应点位置是解题关键．