题目内容
一元二次方程x2-kx-1=0的根的情况是（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法判断 |
考点：根的判别式
专题：
分析：先计算出△=k2+4，则△＞0，根据△的意义得到方程有两个不相等的实数根，从而得出答案．
解答：解：∵△=（-k）2-4×1×（-1）=k2+4，
∵k2≥0，
∴△＞0，
∴方程有两个不相等的实数根；
故选A．
∵k2≥0，
∴△＞0，
∴方程有两个不相等的实数根；
故选A．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一元二次方程根与系数的关系．
练习册系列答案
相关题目
若tanB=
，则∠B的度数为（ ）
| 3 |
| A、30° | B、60° |
| C、45° | D、15° |
若a2=4，b2=9，且ab＜0，则a-b的值为（ ）
| A、-2 | B、±5 | C、5 | D、-5 |
下列方程中，是二元一次方程的是（ ）
| A、xy=7 |
| B、π+x=7 |
| C、x-y=1 |
| D、3x-24=5y+3x |
下列说法中正确的是（ ）
| A、一个角的补角一定是钝角 |
| B、若∠A+∠B+∠C=90°，则∠A+∠B是∠C的余角 |
| C、互补的两个角不可能相等 |
| D、∠A的补角与∠A的余角的差一定等于直角 |
关于x的一元二次方程x2-（m+n）x+mn=0的根的情况是（ ）
| A、有两个相等的实数根 |
| B、有两个不相等实数根 |
| C、有两个实数根 |
| D、没有实数根 |
下列各式变形正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
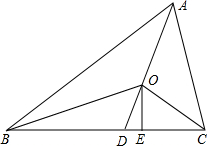如图，O是△ABC的三内角平分线的交点，OE⊥BC．