Question

17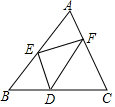．如图，已知D为△ABC的BC边上的一点，DE∥AC交AB于E，DF∥AB交AC于F，求证：△AEF面积为△BDE面积和△CDF面积的比例中项．

Answer 1

分析 作辅助线，构建三角形的高线，根据平行线的距离相等得：DG=FH，EM=DN，证明△EBD∽△FDC，得BE•FC=DE•FD，分别表示△AEF、△BDE、△CDF的面积；利用平行四边形的对边相等得：AE=DF，AF=DE，则AE•AF=DF•DE，与三角形面积相结合得出结论．

解答 解：分别过D、F作AB的垂线DG、FH，垂足为G、H，分别过E、D作AC的垂线EM、DN，垂足为M、N，
∵DF∥AB，DE∥AC，
∴DG=FH，EM=DN，
∠EDB=∠FCB，∠FDC=∠EBC，
∴△EBD∽△FDC，
∴$\frac{BE}{FD}=\frac{DE}{FC}$，
∴BE•FC=DE•FD，
∵S_△AEF•S_AEF=$\frac{1}{2}$AE•FH•$\frac{1}{2}$AF•EM=$\frac{1}{4}$AE•AF•DG•DN，
S_△BED•S_△FDC=$\frac{1}{2}$BE•DG•$\frac{1}{2}$FC•DN=$\frac{1}{4}$DE•FD•DG•DN，
∵DF∥AB，DE∥AC，
∴四边形AEDF是平行四边形，
∴AE=DF，AF=DE，
∴AE•AF=DF•DE，
∴S_△AEF•S_AEF=S_△BED•S_△FDC，
即：△AEF面积为△BDE面积和△CDF面积的比例中项．

点评 本题考查了相似三角形、平行四边形的性质和判定，熟知比例中项的定义：如果a²=bc，则a就是b与c的比例中项；对于三角形相似的判定，常利用平行相似或两角对应相等来证明；本题在计算三角形面积时，要注意两平行线的距离相等．