题目内容
15.求方程x2+12x-5=5$\sqrt{{x}^{2}+12x+9}$的实数根的和与积.分析 令x2+12x-5=y,则原方程可变形为y=5$\sqrt{y+14}$,解方程即可得出y的值,将其代入x2+12x-5=y中利用根与系数的关系即可得出结论.
解答 解:令x2+12x-5=y,则原方程可变形为y=5$\sqrt{y+14}$,
两边开方,整理得:y2-25y-350=0,
解得:y=-10或y=35,
∵$\sqrt{y+14}$非负,
∴y≥0.
∴y=-10(舍去).
∴x2+12x-5=35,即x2+12x-40=0,
∴两根之和为-12,两根之积为-40.
点评 本题考查了换元法解无理方程以及根与系数的关系,利用换元法解无理方程求出x2+12x-5的值是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
4. 实数a,b在数轴上的位置如图,则有( )
实数a,b在数轴上的位置如图,则有( )
 实数a,b在数轴上的位置如图,则有( )
实数a,b在数轴上的位置如图,则有( )| A. | b>a | B. | |a|>|b| | C. | -a<b | D. | -b>a |
5.如果四个各不相等的整数a,b,c,d,它们的积abcd=49,那么a+b+c+d的值为( )
| A. | 14 | B. | -14 | C. | 13 | D. | 0 |
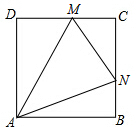 点M、N分别在正方形ABCD的边CD、BC上,已知△MCN的周长等于正方形ABCD周长的一半,求∠MAN的度数.
点M、N分别在正方形ABCD的边CD、BC上,已知△MCN的周长等于正方形ABCD周长的一半,求∠MAN的度数.