题目内容
3．
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c＜0；③a-b+c=-9a；④若（-3，y1），（$\frac{3}{2}$，y2）是抛物线上两点，则y1＞y2，其中正确的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 ①根据直线x=-1是对称轴，确定b-2a的值；
②根据x=-2时，y＞0确定4a-2b+c的符号；
③根据x=-4时，y=0，比较a-b+c与-9a的大小；
④根据抛物线的对称性，得到x=-3与x=1时的函数值相等判断即可．
解答 解：①∵直线x=-1是对称轴，
∴-$\frac{b}{2a}$=-1，即b-2a=0，①正确；
②x=-2时，y＞0，
∴4a-2b+c＞0，②错误；
∵x=-4时，y=0，
∴16a-4b+c=0，又b=2a，
∴a-b+c=-9a，③正确；
④根据抛物线的对称性，得到x=-3与x=1时的函数值相等，
∴y1＞y2，④正确，
故选：C．
点评 本题考查的是二次函数的图象与系数的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．
练习册系列答案
相关题目
16．2015年是第23个“世界水日”，为鼓励居民节约用水，某市规定如下用水收费标准：每户每月的用水量不超过6m3时，水费按a元/立方米收费；超过时，不超过6m3的部分仍按a元/立方米收费，超过的部分按c元/立方米（c＞a）收费，已知该市小明家今年3月份和4月份的用水量、水费如表所示：
（1）求a，c的值；
（2）设某户1个月的用水量为x（m3），应交水费y（元）
①分别写出用水量不超过6m3和超过6m3时，y与x之间的函数关系式；
②已知一户5月份的用水量为8m3，求该户5月份的水费．
| 月份 | 用水量/m3 | 水费/元 |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
（2）设某户1个月的用水量为x（m3），应交水费y（元）
①分别写出用水量不超过6m3和超过6m3时，y与x之间的函数关系式；
②已知一户5月份的用水量为8m3，求该户5月份的水费．
14．
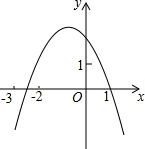已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列四个结论：①b＜0；②c＞1；③b2-4ac＞0；④a-b+c＜0；⑤a+b+1＜0．其中正确的个数有（ ）
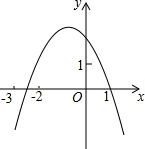已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列四个结论：①b＜0；②c＞1；③b2-4ac＞0；④a-b+c＜0；⑤a+b+1＜0．其中正确的个数有（ ）| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |
18．若一个多边形的每个内角都等于150°，则这个多边形的边数是（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
8．
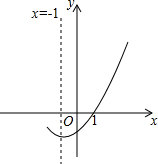如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：
①abc＞0；②ax2+bx+c=0的两根分别为-3和1；③b＞2a；④-2b+c＜0；
其中正确的命题是（ ）
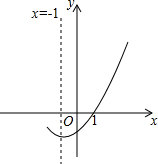如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①abc＞0；②ax2+bx+c=0的两根分别为-3和1；③b＞2a；④-2b+c＜0；
其中正确的命题是（ ）
| A． | ①② | B． | ②④ | C． | ①③ | D． | ③④ |
如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分．已知抛物线的对称轴为x=2，它与x轴的一个交点是（-1，0）．则抛物线与x轴的另一个交点是（5，0）；a+b+c＜0（填“＜或=或＞”）