题目内容
11．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0）、（2，0）、（2，1）、（3，1）、（3，0）、（3，-1）…根据这个规律探索可得，第37个点的坐标为（9，4）．
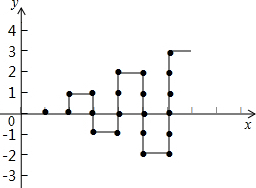
分析 图中可以看出横坐标为1的有一个点，横坐标为2的有2个点，横坐标为3的有3个点，…依此类推横坐标为n的有n个点．进一步通过加法计算算出第37个点位于第几列第几行，然后对应得出坐标规律，将行列数代入规律式．
解答 解：在横坐标上，第一列有一个点，第二列有2个点…第n个有n个点，
并且奇数列点数对称而偶数列点数y轴上方比下方多一个，
所以奇数列的坐标为（n，$\frac{n-1}{2}$）（n，$\frac{n-1}{2}$-1）…（n，$\frac{1-n}{2}$）；
偶数列的坐标为（n，$\frac{n}{2}$）（n，$\frac{n}{2}$-1）…（n，1-$\frac{n}{2}$），
由加法推算可得到第37个点位于第9列自上而下第1行．
代入上式得（9，$\frac{9-1}{2}$）即（9，4），
故答案为：（9，4）．
点评 此题主要考查了点的变化规律，此题的考点在于对坐平面直角坐标系的熟练运用能力，学生也可从其它方面入手寻找规律．
练习册系列答案
相关题目
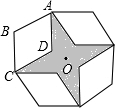如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=1，则图中阴影部分的面积为3-$\sqrt{3}$．
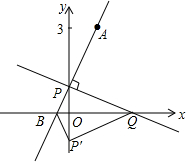如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（1，3），点P的坐标是（0，b）（b＞0且b≠3），直线AP交x轴于点B，过点P作PQ⊥AP，交x轴于点Q，点Q的坐标是（m，0），记点P关于x轴的对称点为P′，连接QP′、BP′．
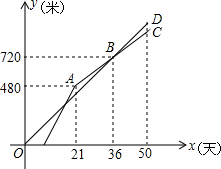甲、乙两个工程队共同开凿一条隧道，甲对按一定的工作效率先施工，一段时间后，乙队从隧道的另一端按一定的工作效率加入施工，中途乙队遇到碎石层，工作效率降低，当乙队完成碎石层时恰好隧道被打通，此时甲队工作了50天．设甲、乙两队各自开凿隧道的长度为y（米），甲对的工作时间为x（天），y与x之间的函数图象如图所示．
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c＜0；③a-b+c=-9a；④若（-3，y1），（$\frac{3}{2}$，y2）是抛物线上两点，则y1＞y2，其中正确的个数是（ ）