题目内容
8．
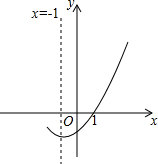如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①abc＞0；②ax2+bx+c=0的两根分别为-3和1；③b＞2a；④-2b+c＜0；
其中正确的命题是（ ）
| A． | ①② | B． | ②④ | C． | ①③ | D． | ③④ |
分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解答 解：①抛物线开口向上，a＞0，
抛物线与y轴交于负半轴，c＜0，
对称轴在y轴的左侧，b＞0，
∴abc＜0，①错误；
②由抛物线的对称性可知，
ax2+bx+c=0的两根分别为-3和1，②正确；
③对称轴-$\frac{b}{2a}$=-1，b=2a，③错误；
④x=-2时，y＜0，
4a-2b+c＜0，
-2b+c＜-4a，4a＞0，
∴-2b+c＜0，④正确，
故选：B．
点评 本题考查的是二次函数图象与系数的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定，二次函数y=ax2+bx+c与x轴交点的横坐标即为方程ax2+bx+c=0的两个根．
练习册系列答案
相关题目
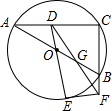如图，⊙O是△ABC的外接圆，AB为直径，过点O作OD∥BC，交AC于点D．
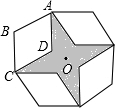如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=1，则图中阴影部分的面积为3-$\sqrt{3}$．
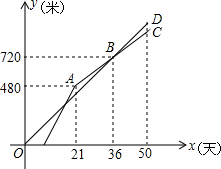甲、乙两个工程队共同开凿一条隧道，甲对按一定的工作效率先施工，一段时间后，乙队从隧道的另一端按一定的工作效率加入施工，中途乙队遇到碎石层，工作效率降低，当乙队完成碎石层时恰好隧道被打通，此时甲队工作了50天．设甲、乙两队各自开凿隧道的长度为y（米），甲对的工作时间为x（天），y与x之间的函数图象如图所示．
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c＜0；③a-b+c=-9a；④若（-3，y1），（$\frac{3}{2}$，y2）是抛物线上两点，则y1＞y2，其中正确的个数是（ ）