题目内容
△ABC中，∠A=100°，∠B、∠C的角平分线交于点O，则∠BOC= ．
考点：三角形内角和定理
专题：
分析：根据题意画出图形，根据三角形内角和定理可求得∠ABC+∠ACB的度数，再根据角平分线的定义可求得∠OBC+∠OCB的度数故可得出结论．
解答：解：如图所示：
∵∠A=100°，
∴∠ABC+∠ACB=80°，
∵点O是∠ABC与∠ACB的角平分线的交点，
∴∠OBC+∠OCB=40°，
∴∠BOC=140°．
故答案为：140°．
∵∠A=100°，
∴∠ABC+∠ACB=80°，
∵点O是∠ABC与∠ACB的角平分线的交点，
∴∠OBC+∠OCB=40°，
∴∠BOC=140°．
故答案为：140°．
点评：本题考查的是三角形内角和定理，即三角形的内角和为180°．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如图，矩形ABCD中，将四边形ABEF沿EF折叠得到四边形HGFE，已知∠CFG=40°，则∠DEF=下列函数中，y随x的增大而减小的是（ ）
A、y=
| ||
| B、y=0.02x | ||
| C、y=x+1 | ||
| D、y=2-3x |
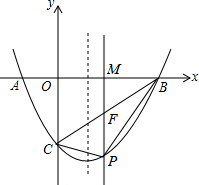在平面直角坐标系中，A（-1，0），C（0，-2），点B在x轴上，抛物线过A、B、C三点且对称轴为直线x=
已知：如图，将三个全等的正方形拼成一个矩形ABGH．求证：∠1+∠2=45°．如果两个角的两边互相平行，那么这两个角（ ）
| A、相等 | B、互余 |
| C、相等或互补 | D、互补 |
