题目内容
 如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?
如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?考点:一元二次方程的应用
专题:几何图形问题
分析:根据可以砌60m长的墙的材料,即总长度是60m,BC=xm,则AB=
(60-x+2)m,再根据矩形的面积公式列方程,解一元二次方程即可.
| 1 |
| 2 |
解答:解:设矩形花园BC的长为x米,则其宽为
(60-x+2)米,依题意列方程得:
(60-x+2)x=300,
x2-62x+600=0,
解这个方程得:x1=12,x2=50,
∵28<50,
∴x2=50(不合题意,舍去),
∴x=12.
(60-x+2)x=480,
x2-62x+960=0,
解这个方程得:x1=32,x2=30,
∵28<30<32,
∴x1=32,x2=30(不合题意,舍去),
答:当矩形的长BC为12米时,矩形花园的面积为300平方米;不能围成480平方米的矩形花园.
| 1 |
| 2 |
| 1 |
| 2 |
x2-62x+600=0,
解这个方程得:x1=12,x2=50,
∵28<50,
∴x2=50(不合题意,舍去),
∴x=12.
| 1 |
| 2 |
x2-62x+960=0,
解这个方程得:x1=32,x2=30,
∵28<30<32,
∴x1=32,x2=30(不合题意,舍去),
答:当矩形的长BC为12米时,矩形花园的面积为300平方米;不能围成480平方米的矩形花园.
点评:本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系求解,注意围墙EF最长可利用28m,舍掉不符合题意的数据.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
如果两个角的两边互相平行,那么这两个角( )
| A、相等 | B、互余 |
| C、相等或互补 | D、互补 |
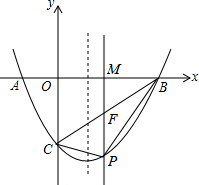 在平面直角坐标系中,A(-1,0),C(0,-2),点B在x轴上,抛物线过A、B、C三点且对称轴为直线x=
在平面直角坐标系中,A(-1,0),C(0,-2),点B在x轴上,抛物线过A、B、C三点且对称轴为直线x=