题目内容
15．
如图，在⊙O中，AB是直径，AC是弦，连接OC，若∠ACO=30°，则∠BOC的度数是（ ）| A． | 30° | B． | 45° | C． | 55° | D． | 60° |
分析 由等腰三角形的性质得出∠A=∠ACO=30°，再由圆周角定理即可得出答案．
解答 解：∵OA=OC，
∴∠A=∠ACO=30°，
∵AB是⊙O的直径，
∴∠BOC=2∠A=2×30°=60°．
故选D．
点评 此题考查了圆周角定理、等腰三角形的性质．熟练掌握圆周角定理是解决问题的关键．
练习册系列答案
相关题目
6．直线y=2x-3与y=-x+3的交点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．已知二次函数y=x2-2mx（m为常数），当-1≤x≤2时，函数值y的最小值为-2，则m的值是（ ）
| A． | $\frac{3}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{3}{2}$或$\sqrt{2}$ | D． | $-\frac{3}{2}$或$\sqrt{2}$ |
10．下列计算正确的是（ ）
| A． | 2a×3a=5a | B． | （-2a）3=-6a3 | C． | 6a÷2a=3a | D． | （-a3）2=a6 |
7．下列运算正确的是（ ）
| A． | （a3）2=a5 | B． | a2•a3=a5 | C． | a6÷a2=a3 | D． | 3a2-2a2=1 |
4．在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（ ）
| A． | 22 | B． | 20 | C． | 22或20 | D． | 18 |
12．
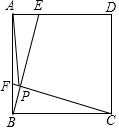如图，点E、F是边长为4的正方形ABCD边AD、AB上的动点，且AF=DE，BE交CF于点P，在点E、F运动的过程中，PA的最小值为（ ）
如图，点E、F是边长为4的正方形ABCD边AD、AB上的动点，且AF=DE，BE交CF于点P，在点E、F运动的过程中，PA的最小值为（ ）| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4$\sqrt{2}$-2 | D． | 2$\sqrt{5}$-2 |