题目内容
10.若方程x2-3x+2=0的两根是等腰三角形两边的长,则该三角形的周长是5.分析 因式分解法解方程得出x的值,再根据等腰三角形的性质分类讨论,利用三角形三边之间的关系检验可得答案.
解答 解:∵x2-3x+2=0,
∴(x-1)(x-2)=0,
∴x-1=0或x-2=0,
解得:x=1或x=2,
当三角形的三边为1、1、2时,1+1=2,不能构成三角形,舍去;
当三角形的三边为1、2、2时,1+2>2,可以构成三角形,其周长为5,
故答案为:5.
点评 本题主要考查因式分解法解一元二次方程、等腰三角形的性质及三角形三边之间的关系,根据等腰三角形的性质分类讨论,并利用三角形三边之间的关系检验是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1.将面积为a2的正方形边长增加3,则正方形的面积增加了( )
| A. | 9 | B. | 2a+9 | C. | 3a+9 | D. | 6a+9 |
5.在实数$\frac{11}{7}$、$-\sqrt{3}$、$\root{3}{9}$、0、π中,无理数有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.由于夏季电力供应紧张,某地决定对工厂实行鼓励错峰用电,规定:在每天的7:00至24:00为用电高峰期,电价为a元/度;每天00:00至7:00为用电平稳期,电价为0.2元/度,下表为某厂7、8月份的用电量和电费的情况统计表:
(1)若7月份在平稳期的用电量占当月总用电量的$\frac{1}{3}$,求a的值;
(2)若a=0.6,则8月份在平稳期的用电量占当月总用电量的多少?
| 月份 | 总用电量(万度) | 电费(万元) |
| 7 | 12 | 6.4 |
| 8 | 16 | 8.8 |
(2)若a=0.6,则8月份在平稳期的用电量占当月总用电量的多少?
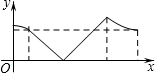
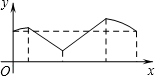
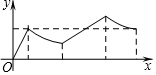
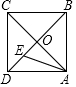 如图,正方形ABCD的边长为a,AC与BD交于点O,E为OD中点,动点P从点O出发,沿折O→E→A→B→O的路径运动,回到点O时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是 ( )
如图,正方形ABCD的边长为a,AC与BD交于点O,E为OD中点,动点P从点O出发,沿折O→E→A→B→O的路径运动,回到点O时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是 ( )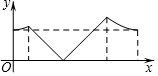
 如图,已知BEFG是长方形,A为EB延长线上一点,AF交BG于点C,D为AC上一点,且AD=BD=BF,若∠BFG=60°,则∠AFG的度数为20°.
如图,已知BEFG是长方形,A为EB延长线上一点,AF交BG于点C,D为AC上一点,且AD=BD=BF,若∠BFG=60°,则∠AFG的度数为20°.