关于抛物线y=(x-1)2-2.下列说法错误的是( )A．顶点坐标为B．函数有最小值为-2C．开口方向向上D．当x＞1时.y随x的增大而减小题目和参考答案——青夏教育精英家教网—

题目内容

7．关于抛物线y=（x-1）²-2，下列说法错误的是（　　）

	A．	顶点坐标为（1，-2）		B．	函数有最小值为-2
	C．	开口方向向上		D．	当x＞1时，y随x的增大而减小

分析已知抛物线解析式为顶点式，根据顶点式的特点判断顶点坐标，开口方向，最值及增减性．

解答解：由抛物线y=（x-1）²-2可知，
顶点坐标为（1，-2），
抛物线开口向上，函数有最小值为-2，
x＞1时y随x增大而增大，
∴A、B、C判断正确，D错误．
故选D．

点评本题考查了二次函数的性质．关键是熟练掌握顶点式与抛物线开口方向，增减性，顶点坐标及最大（小）值之间的联系．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

相关题目

	A．	3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$		B．	$\sqrt{（-9）×（-25）}=\sqrt{9}×\sqrt{-25}=（-3）×（-5）=15$
	C．	-3$\sqrt{\frac{2}{3}}$=$\sqrt{{{（-3）}^2}×\frac{2}{3}}$=6		D．	$\sqrt{{{13}^2}-{{12}^2}}=\sqrt{（13+12）（13-12）}$=5

18．若$\frac{a}{3}$+1与$\frac{2a+1}{3}$的绝对值相等，则a的值为（　　）

15．材料阅读：
将分式$\frac{{x}^{2}+2x-5}{x+3}$拆分成一个整式与一个分式（分子为整数）的和（差）的形式．
解：由分母为x+3，可设x²+2x-5=（x+3）（x+a）+b，
则由x²+2x-5=（x+3）（x+a）+b=x²+ax+3x+3a+b=x²+（a+3）x+（3a+b）．
∵对于任意x，上述等式均成立，∴$\left\{\begin{array}{l}{a+3=2}\\{3a+b=-5}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$．
∴$\frac{{x}^{2}+2x-5}{x+3}$=$\frac{（x+3）（x-1）-2}{x+3}$=$\frac{（x+3）（x-1）}{x+3}$-$\frac{2}{x+3}$=x-1-$\frac{2}{x+3}$
这样，分式$\frac{{x}^{2}+2x-5}{x+3}$就被拆分成一个整式与一个分式（分子为整数）的和（差）的形式．
（1）将分式$\frac{{x}^{2}+3x+6}{x-1}$拆分成一个整式与一个分式（分子为整数）的和（差）的形式；
（2）将分式$\frac{-2{x}^{4}-{x}^{2}+5}{-{x}^{2}+1}$拆分成整式与一个分式（分子为整数）的和（差）的形式．

2．已知m是-2的相反数，n是-1的倒数，则（m+n）²⁰¹⁶=1．

12．下列计算正确的是（　　）

A．

$\sqrt{20}=2\sqrt{10}$

B．

$\sqrt{4}-\sqrt{2}$=$\sqrt{2}$

C．

$\sqrt{2}×\sqrt{3}=\sqrt{6}$

x⁵÷x^-1=x⁴

（x⁴）⁴=x¹⁶

16．

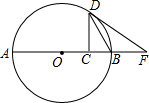如图，点D在⊙O上，过点D的切线交直径AB延长线于点P，DC⊥AB于点C．
（1）求证：DB平分∠PDC；
（2）若DC=6，tan∠P=$\frac{3}{4}$，求BC的长．

17．

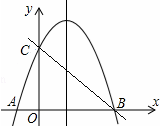如图，抛物线y=-x²+3x+4交x轴于A、B两点（点A在B左边），交y轴于点C．
（1）求A、B两点的坐标；
（2）求直线BC的函数关系式；
（3）点P在抛物线的对称轴上，连接PB，PC，若△PBC的面积为4，求点P的坐标．

试题分类