题目内容
如图1,△ABC中,BE平分∠ABC交AC边于点E,过点E作DE∥BC交AB于点D,
(1)求证:△BDE为等腰三角形;
(2)若点D为AB中点,AB=6,求线段BC的长;
(3)在图2条件下,若∠BAC=60°,动点P从点B出发,以每秒1个单位的速度沿射线BE运动,请直接写出图3当△ABP为等腰三角形时t的值.

(1)求证:△BDE为等腰三角形;
(2)若点D为AB中点,AB=6,求线段BC的长;
(3)在图2条件下,若∠BAC=60°,动点P从点B出发,以每秒1个单位的速度沿射线BE运动,请直接写出图3当△ABP为等腰三角形时t的值.

考点:等腰三角形的判定与性质,勾股定理
专题:
分析:(1)由角平分线和平行线的性质可得到∠BDE=∠DEB,可证得结论;
(2)由条件可知BD=DE=DA=3,且DE为△ABC的中位线,可求得BC长;
(3)分BP=AP、BP=AB、AP=AB三种情况分别讨论求t的值即可.
(2)由条件可知BD=DE=DA=3,且DE为△ABC的中位线,可求得BC长;
(3)分BP=AP、BP=AB、AP=AB三种情况分别讨论求t的值即可.
解答:(1)证明:
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵DE∥BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形;
(2)解:
∵点D为AB中点
∴AD=BD=ED=
AB=3,
∵DE∥BC,
∴E为AC中点,
∴DE为△ABC的中位线,
∴BC=2DE=6;
(3)在(2)的条件下可知DE=DA,且∠BAC=60°,
∴△ADE为等边三角形,
∵BC=2DE=AB,
∴△ABC为等边三角形,
当BP=AP时,过点P作PE⊥AB,交AB于点E,则BF=
AB=6,

在Rt△PBF中,∠PBF=
∠ABC=30°,
∴BP=2
,即t=2
,
当BP=BA时,此时BP=6,即t=6,
当AB=AP时,此时,BP=2BE=6
,即t=6
,
综上可知当△ABP为等腰三角形时t的值为2
,6,6
.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵DE∥BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形;
(2)解:
∵点D为AB中点
∴AD=BD=ED=
| 1 |
| 2 |
∵DE∥BC,
∴E为AC中点,
∴DE为△ABC的中位线,
∴BC=2DE=6;
(3)在(2)的条件下可知DE=DA,且∠BAC=60°,
∴△ADE为等边三角形,
∵BC=2DE=AB,
∴△ABC为等边三角形,
当BP=AP时,过点P作PE⊥AB,交AB于点E,则BF=
| 1 |
| 2 |

在Rt△PBF中,∠PBF=
| 1 |
| 2 |
∴BP=2
| 3 |
| 3 |
当BP=BA时,此时BP=6,即t=6,
当AB=AP时,此时,BP=2BE=6
| 3 |
| 3 |
综上可知当△ABP为等腰三角形时t的值为2
| 3 |
| 3 |
点评:本题主要考查等腰三角形的性质和判定及勾股定理、平行线性质的综合应用,掌握等腰三角形的判定方法是解题的关键,在第(3)中注意分情况讨论.

练习册系列答案
相关题目
关于x的一元二次方程x2+x-1=0的两个根分别为a,b,则
+
=( )
| 1 |
| a |
| 1 |
| b |
| A、2 | B、1 | C、-1 | D、-2 |
下列各式正确的是( )
| A、-8-5=-3 |
| B、-5+4=-9 |
| C、-1-1=-2 |
| D、1-2=1 |
 已知在?ABCD中,E是AD延长线上的一点,DE=n•AD,EB和DC相交于点F,求
已知在?ABCD中,E是AD延长线上的一点,DE=n•AD,EB和DC相交于点F,求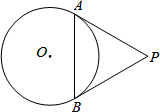 如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是
如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是