题目内容
14.已知△ABC的三边a、b、c满足$|{\frac{1}{2}a-4}|+{(2b-12)^2}+\sqrt{10-c}$=0,求最长边上的高h.分析 根据非负数的性质可得$\frac{1}{2}a-4=0$,2b-12=0,10-c=0,计算出a、b、c的值,再利用勾股定理逆定理可证明△ABC为直角三角形,然后利用直角三角形的面积计算方法可得最长边上的高h的值.
解答 解:由题意,得:$\frac{1}{2}a-4=0$,2b-12=0,10-c=0,
∴a=8,b=6,c=10,
∵a2+b2=64+36=100=c2,
∴△ABC为Rt△ABC,且∠C=90°,
∵$\frac{1}{2}$ch=$\frac{1}{2}$ab,
∴h=4.8.
点评 此题主要考查了非负数的性质,以及勾股定理逆定理,关键是掌握三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.把分式$\frac{x}{y}$中的x,y都扩大2倍,则分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 扩大4倍 | D. | 缩小2 |
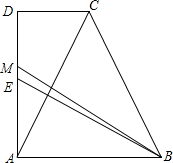 如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.
如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.