Question

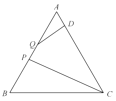
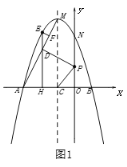
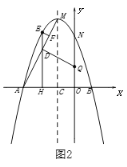
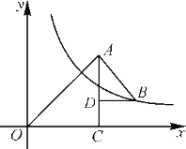
【题目】如图，△OAC和△BAD都是等腰直角三角形，，反比例函数在第一象限的图象经过点B，则S△OAC－S△BAD=（ ）

A.1.5B.2.5C.3D.1

Answer 1

【答案】A

【解析】

设△OAC和△BAD的直角边长分别为a、b，结合等腰直角三角形的性质及图象可得出点B的坐标，根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论．

设△OAC和△BAD的直角边长分别为a、b，

∵△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，

∴点B的坐标为（a＋b，ab），

∵反比例函数在第一象限的图象经过点B，

∴（a＋b）×（ab）＝a2b2＝3．

∴S△OACS△BAD＝a2b2＝（a2b2）＝1.5．

故选：A．