题目内容
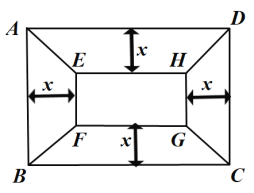
【题目】如图,等边![]() 的边长为3,点
的边长为3,点![]() 在边
在边![]() 上,
上,![]() ,线段
,线段![]() 在边
在边![]() 上运动,
上运动,![]() ,有下列结论:
,有下列结论:
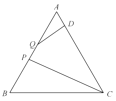
①![]() 与
与![]() 可能相等;②
可能相等;②![]() 与
与![]() 可能相似;③四边形
可能相似;③四边形![]() 面积的最大值为
面积的最大值为![]() ;④四边形
;④四边形![]() 周长的最小值为
周长的最小值为![]() .其中,正确结论的序号为( )
.其中,正确结论的序号为( )
A.①④B.②④C.①③D.②③
【答案】D
【解析】
①通过分析图形,由线段![]() 在边
在边![]() 上运动,可得出
上运动,可得出![]() ,即可判断出
,即可判断出![]() 与
与![]() 不可能相等;
不可能相等;
②假设![]() 与
与![]() 相似,设
相似,设![]() ,利用相似三角形的性质得出
,利用相似三角形的性质得出![]() 的值,再与
的值,再与![]() 的取值范围进行比较,即可判断相似是否成立;
的取值范围进行比较,即可判断相似是否成立;
③过P作PE⊥BC于E,过F作DF⊥AB于F,利用函数求四边形![]() 面积的最大值,设
面积的最大值,设![]() ,可表示出
,可表示出![]() ,
,![]() ,可用函数表示出
,可用函数表示出![]() ,
,![]() ,再根据
,再根据![]() ,依据
,依据![]() ,即可得到四边形
,即可得到四边形![]() 面积的最大值;
面积的最大值;
④作点D关于直线![]() 的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,此时四边形P′CDQ′的周长为:
的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,此时四边形P′CDQ′的周长为:![]() ,其值最小,再由D1Q′=DQ′=D2 P′,
,其值最小,再由D1Q′=DQ′=D2 P′,![]() ,且∠AD1D2=120°,∠D2AC=90°,可得
,且∠AD1D2=120°,∠D2AC=90°,可得![]() 的最小值,即可得解.
的最小值,即可得解.
解:①∵线段![]() 在边
在边![]() 上运动,
上运动,![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 不可能相等,
不可能相等,
则①错误;
②设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
假设![]() 与
与![]() 相似,
相似,
∵∠A=∠B=60°,
∴![]() ,即
,即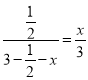 ,
,
从而得到![]() ,解得
,解得![]() 或
或![]() (经检验是原方程的根),
(经检验是原方程的根),
又![]() ,
,
∴解得的![]() 或
或![]() 符合题意,
符合题意,
即![]() 与
与![]() 可能相似,
可能相似,
则②正确;
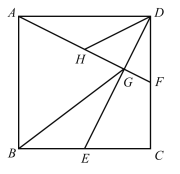
③如图,过P作PE⊥BC于E,过D作DF⊥AB于F,
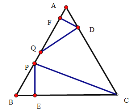
设![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,即
,即![]() ,
,
∴![]() ,
,
∵∠B=60°,
∴![]() ,
,
∵![]() ,∠A =60°,
,∠A =60°,
∴![]() ,
,
则![]() ,
,
![]() ,
,
∴四边形![]() 面积为:
面积为:![]() ,
,
又∵![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 面积最大,最大值为:
面积最大,最大值为:![]() ,
,
即四边形![]() 面积最大值为
面积最大值为![]() ,
,
则③正确;
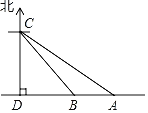
④如图,作点D关于直线![]() 的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,
的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,
此时四边形P′CDQ′的周长为:![]() ,其值最小,
,其值最小,
∴D1Q′=DQ′=D2 P′,![]() ,
,
且∠AD1D2=180![]() ∠D1AB=180
∠D1AB=180![]() ∠DAB =120°,
∠DAB =120°,
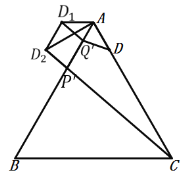
∴∠D1AD2=∠D2AD1=![]() =30°,∠D2AC=90°,
=30°,∠D2AC=90°,
在△D1AD2中,∠D1AD2=30°,![]() ,
,
∴![]() ,
,
在Rt△AD2C中,
由勾股定理可得,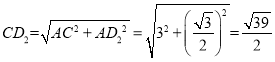 ,
,![]()
∴四边形P′CDQ′的周长为:
![]()
![]()
![]() ,
,
则④错误,
所以可得②③正确,
故选:D.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案