Question

【题目】（问题背景）在面积都相等的所有矩形中，当其中一个矩形的一边长为时，它的另一边长为．求周长的取值范围．

（建立模型）

（1）设矩形相邻两边的长分别为，，由题意可得，则，由周长为，得，即，满足要求的的取值，从“图形”角度考虑，应是函数与 的图象在第一象限内有公共点时的取值范围；从“代数”角度考虑，应看作方程 有正数解时的取值范围．

（画图观察）

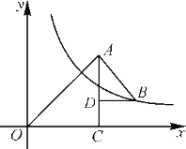
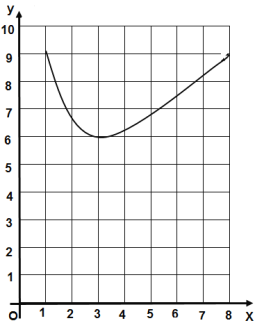
（2）函数的图象如图所示，而函数的图象是一条与轴平行的直线．当直线与函数的图象有唯一公共点（ ， ）时，周长取得最小值为 ．

（代数说理）

（3）圆圆说矩形的周长可以为，方方说矩形的周长可以为，你认为圆圆和方方的说法对吗？为什么？

Answer 1

【答案】（1），；（2），，；（3）矩形的周长为，方方的说法对，理由见解析

【解析】

（1）此题要读懂题意，从图形的角度去考虑应该是两条函数图象：与的图象在第一象限内有公共点时的取值范围；从“代数”角度考虑，应看作方程有正数解时的取值范围；

（2）画出直线与有唯一公共点（3，6）即可解答问题；

（3）由（2）可知此矩形周长最小值为12，故圆圆的说法错误，方方的说法是有理的，可以通过解方程进行说明.

解（1）；

（2）如图，

由图象可以看出，直线与函数的图象有唯一公共点（3，6），周长最小值为：，即m=12；

故答案为：，，；

（3）由（2）知，此矩形的周长最小值为12，圆圆说矩形的周长可以为，是错误的，方方说矩形的周长可以为，是有道理的.

理由：若矩形的周长为

则

即

整理，得

方程无解

故矩形的周长不可能为，圆圆的说法不对

若矩形的周长为

则

即

整理，得

方程有两个不相等的实数根

故矩形的周长为，方方的说法对