题目内容
8.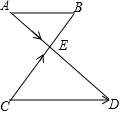 如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.
如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.
分析 根据$\overrightarrow{CD}$=$\overrightarrow{CE}$+$\overrightarrow{ED}$,只要求出$\overrightarrow{ED}$即可解决问题.
解答 解: ∵AB∥CD,
∵AB∥CD,
∴$\frac{AB}{CD}$=$\frac{AE}{ED}$=$\frac{1}{2}$,
∴ED=2AE,
∵$\overrightarrow{AE}$=$\overrightarrow{a}$,
∴$\overrightarrow{ED}$=2$\overrightarrow{a}$,
∴$\overrightarrow{CD}$=$\overrightarrow{CE}$+$\overrightarrow{ED}$=$\overrightarrow{b}$+2$\overrightarrow{a}$.
点评 本题考查平面向量、平行线的性质等知识,解题的关键是熟练掌握三角形法则求向量,属于基础题.

练习册系列答案
相关题目
18.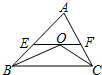 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. |  | B. |  | C. | 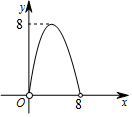 | D. | 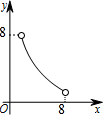 |
19. 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |
20.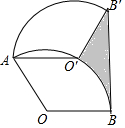 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$ | B. | 2$\sqrt{3}$-$\frac{π}{3}$ | C. | 2$\sqrt{3}$-$\frac{2π}{3}$ | D. | 4$\sqrt{3}$-$\frac{2π}{3}$ |
17.下列哪一个是假命题( )
| A. | 五边形外角和为360° | |
| B. | 切线垂直于经过切点的半径 | |
| C. | (3,-2)关于y轴的对称点为(-3,2) | |
| D. | 抛物线y=x2-4x+2017对称轴为直线x=2 |
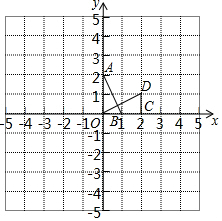 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.
如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.