题目内容
15.关于x的方程4x2-(k+2)x+1=-1有两个相等根,求k的值并求x.分析 先根据题意得出△=0,求出k的值,代入原方程求出x的值即可.
解答 解:原方程可化为4x2-(k+2)x+2=0,
∵关于x的方程4x2-(k+2)x+1=-1有两个相等根,
∴△=0,即△=[-(k+2)]2-4×4×2=0,解得k=-2±4$\sqrt{2}$.
当k=-2+4$\sqrt{2}$时,原程可化方为4x2-4$\sqrt{2}$x+2=0,解得x=$\frac{\sqrt{2}}{2}$;
当k=-2-4$\sqrt{2}$时,原程可化方为4x2+4$\sqrt{2}$x+2=0,解得x=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是根的判别式,熟知一元二次方程的根与判别式的关系是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.两直线相交形成的4个角的度数之比依次可能是( )
| A. | 2:3:2:3 | B. | 1:1:4:4 | C. | 1:2:3:4 | D. | 3:4:4:3 |
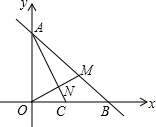 如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4.
如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.