Question

已知△ABC中，AB=6，AC=5，BC边上的高AD=4，求BC的长．

Answer 1

考点：勾股定理

专题：计算题

分析：分两种情况考虑：如图1所示，此时△ABC为锐角三角形，在直角三角形ABD与直角三角形ACD中，利用勾股定理求出BD与DC的长，由BD+DC求出BC的长即可；如图2所示，此时△ABC为钝角三角形，同理由BD-CD求出BC的长即可．

解答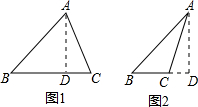：解：分两种情况考虑：
如图1所示，此时△ABC为锐角三角形，
在Rt△ABD中，根据勾股定理得：BD=

AB2-AD2

=

36-16

=2

5

；
在Rt△ACD中，根据勾股定理得：CD=

AC2-AD2

=

25-16

=3，
此时BC=BD+DC=2

5

+3；
如图2所示，此时△ABC为钝角三角形，
在Rt△ABD中，根据勾股定理得：BD=

AB2-AD2

=

36-16

=2

5

；
在Rt△ACD中，根据勾股定理得：CD=

AC2-AD2

=

25-16

=3，
此时BC=BD-DC=2

5

-3，
综上，BC的长为2

5

+3或2

5

-3．

点评：此题考查了勾股定理，利用了分类讨论的思想，熟练掌握勾股定理是解本题的关键．